Section : Caractérisation des processus MA
Précédent : Preuve de la proposition
Suivant : Exercice 9.
Soit 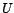 une variable aléatoire. On sait que
une variable aléatoire. On sait que
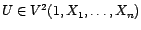 si et
seulement si
si et
seulement si
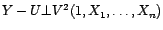 et
et
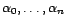 : autrement
dit, si et seulement s'il existe
: autrement
dit, si et seulement s'il existe
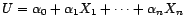 tel que
et
Rappelons que
tel que
et
Rappelons que
![$ \langle A,B\rangle={\mathbb{E}}\left[AB\right]$](img599.gif) , et que
, et que
![$ {\mathbb{E}}\left[AB\right]=\mathop{\hbox{\upshape {cov}}}\nolimits (A,B)$](img600.gif) si
si 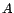 est une variable aléatoire
centrée. On en déduit que
est une variable aléatoire
centrée. On en déduit que
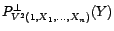 est
égal à
est
égal à
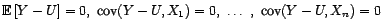 si et
seulement si
ou encore
En remplaçant
si et
seulement si
ou encore
En remplaçant 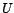 par
par
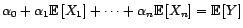 , cette
condition devient
et
Ce qui sont les formules attendues.
, cette
condition devient
et
Ce qui sont les formules attendues.
Thierry Cabanal-Duvillard
![$\displaystyle {\alpha}_0+{\alpha}_1{\mathbb{E}}\left[X_1\right]+\cdots+{\alpha}_n{\mathbb{E}}\left[X_n\right]={\mathbb{E}}\left[Y\right] $](img606.gif)