Section : Caractérisation des processus MA
Précédent : Preuve du lemme .
Suivant : Preuve
du corollaire .
Montrer que la matrice de covariance de
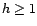 n'est pas inversible si et
seulement si
n'est pas inversible si et
seulement si
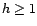 est une famille affinement
liée.
est une famille affinement
liée.
Corollaire 2.I.6
Soient  un processus faiblement stationnaire et
un processus faiblement stationnaire et
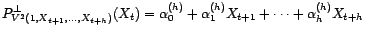 . Alors, quel que soit
. Alors, quel que soit
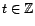 ,
Le système linéaire (
,
Le système linéaire (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) porte le nom
d'équations de Yule-Walker.
) porte le nom
d'équations de Yule-Walker.
Thierry Cabanal-Duvillard