Section : Mathématiques des marchés
financiers
Précédent : Théorème
Suivant : Théorème
Nous en arrivons à la question centrale : à quel prix
doit on vendre une option européenne 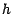 ? La
première estimation qui vient à l'esprit est la
valeur moyenne de l'option à sa date d'exercice , à
savoir
? La
première estimation qui vient à l'esprit est la
valeur moyenne de l'option à sa date d'exercice , à
savoir
![$ \textbf{E}[h]$](img1071.gif) ; c'est oublier que la vente
de l'option procure à son émetteur , dès
l'instant 0 , une somme d'argent qu'il peut faire fructifier
à sa guise ; il peut, par exemple, placer cet argent
à la caisse d'épargne et, dans cette
hypothèse, se permettre de vendre moins cher, au prix
; c'est oublier que la vente
de l'option procure à son émetteur , dès
l'instant 0 , une somme d'argent qu'il peut faire fructifier
à sa guise ; il peut, par exemple, placer cet argent
à la caisse d'épargne et, dans cette
hypothèse, se permettre de vendre moins cher, au prix
![$\displaystyle \beta_N \textbf{E}[h]=\textbf{E}[\tilde h]=\frac{1}{({1+r})^N} \textbf{E}[h]$](img1072.gif)
|
(4.32) |
Mais, dans un marché complet, il peut faire mieux : il a
(au moins théoriquement) la possibilité de simuler
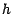 s'il consent à investir dans des
actifs à risque ; il dispose ainsi d'une stratégie
s'il consent à investir dans des
actifs à risque ; il dispose ainsi d'une stratégie
 (appelée stratégie de
couverture de l'option) lui permettant de constituer un
portefeuille dont la valeur à l'instant
(appelée stratégie de
couverture de l'option) lui permettant de constituer un
portefeuille dont la valeur à l'instant 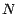 est exactement
est exactement 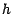 . Il est donc naturel de
définir le prix
. Il est donc naturel de
définir le prix 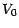 de l'option
de l'option 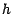 à l'instant 0 et son prix
à l'instant 0 et son prix 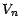 à l'instant
à l'instant  par
par
On notera que 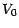 est une constante , (c'est le prix
conseillé à l'émetteur de l'option) , tandis
que
est une constante , (c'est le prix
conseillé à l'émetteur de l'option) , tandis
que 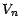 est une variable aléatoire
est une variable aléatoire
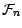 -mesurable , c'est à dire
une fonction de l'évolution des cours observés
jusqu'à la date
-mesurable , c'est à dire
une fonction de l'évolution des cours observés
jusqu'à la date  , (dans les cas usuels ce
sera une fonction du dernier cours
, (dans les cas usuels ce
sera une fonction du dernier cours 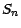 ) , ce qui
parait raisonnable .
) , ce qui
parait raisonnable .
Dans la réalité, notre option 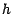 sera mise sur le marché tout comme une action, et deviendra
ainsi un actif à risque supplémentaire ; elle aura un
prix
sera mise sur le marché tout comme une action, et deviendra
ainsi un actif à risque supplémentaire ; elle aura un
prix 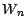 à l'instant
à l'instant  (
différent de
(
différent de 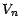 ) déterminé
par la loi de l'offre et de la demande .
) déterminé
par la loi de l'offre et de la demande . 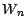 est
la somme d'argent qu'il vous faudra débourser s'il vous
prend la fantaisie d'acheter cette option à la date
est
la somme d'argent qu'il vous faudra débourser s'il vous
prend la fantaisie d'acheter cette option à la date  ; que peut on penser s'il existe un écart
important entre
; que peut on penser s'il existe un écart
important entre 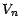 et
et 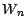 ? Trois
choses différentes suivant les tempéraments :
? Trois
choses différentes suivant les tempéraments :
- que l'on a perdu son temps en lisant ces notes qui exposent une
théorie totalement étrangère aux
réalités du marché .
- que la théorie probabiliste est valide mais que les
statisticiens ont mal fait leur travail : la loi de
probabilité
 gouvernant le cours des actifs
est incorrecte .
gouvernant le cours des actifs
est incorrecte .
- que le marché a tort parce qu'il ne saurait avoir raison
contre un raisonnement mathématique ; si vous observez
à la date
 un prix
un prix 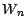 très inférieur à
très inférieur à 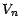 , vous
investissez alors votre fortune et celle de toute votre famille
dans l'option
, vous
investissez alors votre fortune et celle de toute votre famille
dans l'option 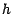 .
.
Bien entendu, si les opérateurs utilisent ces modèles
, c'est parce que les prix qu'ils permettent de calculer ne sont
pas trop éloignés des prix réels
constatés sur les marchés financiers ; mais il est de
mauvais esprits pour prétendre que n'importe quelle formule
magique fournie par une cartomancienne ou un astrologue aboutirait
au même résultat , pourvu que tous les
opérateurs soient convaincus de sa pertinence : si la
totalité d'entre eux sont persuadés qu'il existe un
"juste prix" pour une option, c'est évidemment à ce
prix là que s'effectueront les transactions. Mais revenons
aux mathématiques ; on a le résultat suivant :
Sous-sections
Section : Mathématiques des marchés
financiers
Précédent : Théorème
Suivant : Théorème
Jacques Azéma
![]() s'il consent à investir dans des
actifs à risque ; il dispose ainsi d'une stratégie
s'il consent à investir dans des
actifs à risque ; il dispose ainsi d'une stratégie
![]() (appelée stratégie de
couverture de l'option) lui permettant de constituer un
portefeuille dont la valeur à l'instant
(appelée stratégie de
couverture de l'option) lui permettant de constituer un
portefeuille dont la valeur à l'instant ![]() est exactement
est exactement ![]() . Il est donc naturel de
définir le prix
. Il est donc naturel de
définir le prix ![]() de l'option
de l'option ![]() à l'instant 0 et son prix
à l'instant 0 et son prix ![]() à l'instant
à l'instant ![]() par
par
![]() sera mise sur le marché tout comme une action, et deviendra
ainsi un actif à risque supplémentaire ; elle aura un
prix
sera mise sur le marché tout comme une action, et deviendra
ainsi un actif à risque supplémentaire ; elle aura un
prix ![]() à l'instant
à l'instant ![]() (
différent de
(
différent de ![]() ) déterminé
par la loi de l'offre et de la demande .
) déterminé
par la loi de l'offre et de la demande . ![]() est
la somme d'argent qu'il vous faudra débourser s'il vous
prend la fantaisie d'acheter cette option à la date
est
la somme d'argent qu'il vous faudra débourser s'il vous
prend la fantaisie d'acheter cette option à la date ![]() ; que peut on penser s'il existe un écart
important entre
; que peut on penser s'il existe un écart
important entre ![]() et
et ![]() ? Trois
choses différentes suivant les tempéraments :
? Trois
choses différentes suivant les tempéraments :