Section : Martingales et marchés complets
Précédent : Martingales et marchés complets
Suivant : Prix
et couverture d'une
Un marché viable est complet si et seulement s'il existe une
probabilité unique sous laquelle les prix
actualisés des actifs sont des martingales
Démonstration: a) Supposons le
marché viable et complet et soit 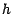 une v.a.r.
une v.a.r.
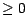 ; il existe une stratégie
admissible
; il existe une stratégie
admissible  telle que
telle que
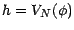 ; comme
; comme  est autofinancée , on peut écrire (cf. la
remarque 4.2.1)
est autofinancée , on peut écrire (cf. la
remarque 4.2.1)
Si
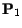 et
et
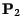 sont deux probabilités
sous lesquelles
sont deux probabilités
sous lesquelles
 est une martingale, on aura
est une martingale, on aura
![$ \beta_N \textbf{E}_1[h]=\beta_N \textbf{E}_2[h]$](img1062.gif) , ce qui
entraine évidemment
, ce qui
entraine évidemment
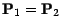
b) Inversement , supposons le marché viable et
non complet ; il exite alors une v.a. 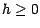 non
simulable ; reprenant les notations du corollaire 4.2.2,
cela signifie que
non
simulable ; reprenant les notations du corollaire 4.2.2,
cela signifie que 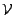 est un sous espace
vectoriel strict de
est un sous espace
vectoriel strict de 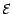 que nous munirons
maitenant du produit scalaire
que nous munirons
maitenant du produit scalaire
![$ <X,Y>=\textbf{E*}[XY]$](img1064.gif) ;
d'après ce que l'on sait des espaces euclidiens, il existe
dans
;
d'après ce que l'on sait des espaces euclidiens, il existe
dans 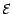 un vecteur
un vecteur  non nul
(i.e. une v.a.r. non nulle) orthogonal à
non nul
(i.e. une v.a.r. non nulle) orthogonal à 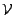 ; cela entraine en particulier, puisque
; cela entraine en particulier, puisque  est orthogonale aux constantes,
est orthogonale aux constantes,
![$ \textbf{E*}[X]=0$](img1065.gif) . Définissons alors
. Définissons alors
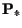 par
l'égalité
par
l'égalité
où 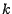 est un réel
est un réel 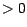 assez grand pour que
assez grand pour que 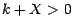 ; il
est alors facile de voir que
; il
est alors facile de voir que
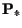 est une probabilité
différente de
est une probabilité
différente de
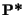 ; de plus, quelque soit la suite
prévisible
; de plus, quelque soit la suite
prévisible 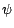 à valeurs dans
à valeurs dans
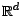 ,
,
Il résulte alors du lemme 3.3.4 que (
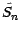 ) est une martingale sous
) est une martingale sous
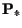 .
.
Section : Martingales et marchés complets
Précédent : Martingales et marchés complets
Suivant : Prix
et couverture d'une
Jacques Azéma
une v.a.r.
; il existe une stratégie admissible
telle que
; comme
est autofinancée , on peut écrire (cf. la remarque 4.2.1)
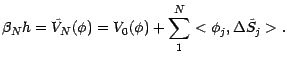
et
sont deux probabilités sous lesquelles
est une martingale, on aura
, ce qui entraine évidemment
non simulable ; reprenant les notations du corollaire 4.2.2, cela signifie que
est un sous espace vectoriel strict de
que nous munirons maitenant du produit scalaire
; d'après ce que l'on sait des espaces euclidiens, il existe dans
un vecteur
non nul (i.e. une v.a.r. non nulle) orthogonal à
; cela entraine en particulier, puisque
est orthogonale aux constantes,
. Définissons alors
par l'égalité
est un réel
assez grand pour que
; il est alors facile de voir que
est une probabilité différente de
; de plus, quelque soit la suite prévisible
à valeurs dans
,
![$\displaystyle \textbf{E}_*[\sum_1^N<\psi_n , \Delta {\tilde S}_n>]=\textbf{E*}[X\sum_1^N <\psi_n , \Delta {\tilde S}_n>]=0.$](img1069.gif)
) est une martingale sous
.