Section : Prix et
couverture d'une
Précédent : Prix et couverture d'une
Suivant : Remarque
![$\displaystyle V_0=\frac{1}{({1+r})^N}\textbf{E*}[h] \hspace{0.5cm};\hspace{0.5cm} V_n=\frac{1}{({1+r})^{N-n}}\textbf{E*}[h\vert {\cal F}_n]$](img1076.gif)
|
(4.33) |
On pourra constater que la faculté donnée au vendeur
de l'option de se couvrir par des actifs à risque se traduit
en langage mathématique par la substitution de
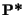 à
à
 ; (comparer
; (comparer 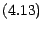 et
et  ) . Le prix d'une option se
calculant à l'aide de
) . Le prix d'une option se
calculant à l'aide de
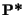 , on peut oublier la
probabilité
, on peut oublier la
probabilité
 , et même dans certains
, et même dans certains
cas , ne pas la connaitre avec précision .Nous allons en
voir un exemple au chapitre suivant.
Démonstration : Puisque
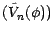 est une martingale sous
est une martingale sous
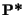 , on a
, on a
Les formules 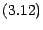 en résultent
immédiatement .
en résultent
immédiatement .
Jacques Azéma
est une martingale sous
, on a
en résultent immédiatement .