Section : Options
simulables (ou réplicables)
Précédent : Le prix d'une option
Suivant : Les
prix d'une option
Soit 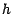 une option européenne
réplicable ;
une option européenne
réplicable ; 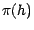 est l'unique prix
excluant l'arbitrage de cette option. Démonstration :
est l'unique prix
excluant l'arbitrage de cette option. Démonstration :
- Montrons d'abord que
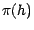 est un p.e.a. de
l'option
est un p.e.a. de
l'option 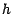 ; revenons aux notations de
; revenons aux notations de ![[*]](file:/usr/share/latex2html/icons/crossref.gif) et posons
et posons
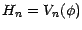 .
Soit d'autre part
.
Soit d'autre part
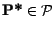 ; comme
; comme
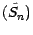 et
et
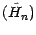 sont des
P*-martingales, il en est de même de
sont des
P*-martingales, il en est de même de
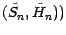 . Il en
résulte que le marché financier étendu
. Il en
résulte que le marché financier étendu
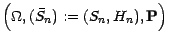 est viable.
est viable.
- Passons à l'unicité ; désignons par
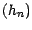 une suite adaptée de v.a.r.
une suite adaptée de v.a.r.
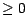 vérifiant
vérifiant 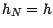 et posons
et posons
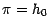 . Nous allons montrer
que, si
. Nous allons montrer
que, si
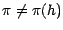 , on peut construire une
statégie d'arbitrage dans le marché financier
étendu
, on peut construire une
statégie d'arbitrage dans le marché financier
étendu
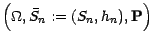 . (
On considère maintenant que l'option, introduite dans le
marché, constitue un actif à risque
supplémentaire noté
. (
On considère maintenant que l'option, introduite dans le
marché, constitue un actif à risque
supplémentaire noté 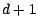 dont le
cours à la date
dont le
cours à la date  est
est  ).
).
Supposons par exemple
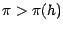 ; posons alors
; posons alors
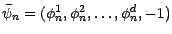 et désignons par
et désignons par
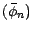 le portefeuille
autofinancé coïncidant avec
le portefeuille
autofinancé coïncidant avec
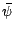 sur les actifs à risque
du marché étendu et vérifiant
sur les actifs à risque
du marché étendu et vérifiant
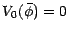 (Cf.
(Cf. ![[*]](file:/usr/share/latex2html/icons/crossref.gif) ). On a
). On a
(4.27) écrite en  conduit à
l'égalité
conduit à
l'égalité
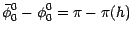 |
(4.28) |
Comme les stratégies
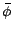 et
et  sont
autofinancées, (4.26) s'écrit encore
sont
autofinancées, (4.26) s'écrit encore
Comparant (4.27) et (4.30), on obtient les relations
Compte tenu de (4.28), on a donc
La stratégie
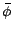 constitue donc un arbitrage qui
peut être mis en pratique de la façon suivante :
constitue donc un arbitrage qui
peut être mis en pratique de la façon suivante :
le spéculateur attiré par la surévaluation de
l'option 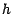 l'emprunte à la date 0, la vend
immédiatement sur le marché au prix
l'emprunte à la date 0, la vend
immédiatement sur le marché au prix 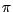 , et prélève sur cette somme la
quantité
, et prélève sur cette somme la
quantité 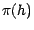 qui lui permet d'acheter le
portefeuille de couverture
qui lui permet d'acheter le
portefeuille de couverture  de l'option
de l'option
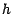 ; la somme restante,
; la somme restante,
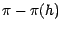 , est placée à la
caisse d'épargne. Après avoir laissé au
lecteur le soin d'imaginer une stratégie d'arbitrage dans le
cas où
, est placée à la
caisse d'épargne. Après avoir laissé au
lecteur le soin d'imaginer une stratégie d'arbitrage dans le
cas où
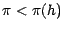 , on conclut qu'on a
nécessirement
, on conclut qu'on a
nécessirement
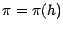 .
.
Section : Options
simulables (ou réplicables)
Précédent : Le prix d'une option
Suivant : Les
prix d'une option
Jacques Azéma