Section : Sratégies autofinancées
Précédent : Remarque:
Suivant : Corollaire :
Proposition:
Soient 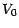 une v.a.r.
une v.a.r.
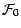 -mesurable (i.e. une constante) et
-mesurable (i.e. une constante) et
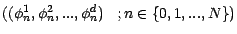 une suite prévisible à valeurs dans
une suite prévisible à valeurs dans
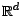 ; il existe stratégie
autofinancée
; il existe stratégie
autofinancée
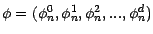 unique telle
que
unique telle
que
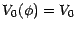 .
.
Démonstration : Si
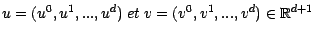 , nous introduirons la notation
, nous introduirons la notation
![$\displaystyle [u,v]=\sum_{k=1}^{k=d}u^kv^k=<u,v>-u^0v^0.$](img825.gif) |
(4.6) |
Si  est une stratégie de
gestion satisfaisant aux conditions de l'énoncé, les
relations (
est une stratégie de
gestion satisfaisant aux conditions de l'énoncé, les
relations (![[*]](file:/usr/share/latex2html/icons/crossref.gif) )
d'éfinissant l'autofinancement sont équivalente aux
égalités
)
d'éfinissant l'autofinancement sont équivalente aux
égalités
qui s'écrivent encore
![$\displaystyle \Delta \phi_{n}^{0}=-[\Delta \phi_{n},\tilde{S}_{n-1}]¥¥$](img827.gif)
|
(4.7) |
On aura en outre
![$\displaystyle V_{0}=V_{0}(\phi)=\phi_{0}^{0}+[\phi_{0},S_{0}]$](img828.gif) |
(4.8) |
ou encore,
![$\displaystyle \phi_{0}^{0}=V_{0}-[\phi_{0},S_{0}]$](img829.gif) |
(4.9) |
Les égalités (4.7) et (4.9) montrent que
la suite
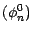 est complètement
déterminée par les suites
est complètement
déterminée par les suites
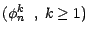 , ce qui montre
l'unicité de
, ce qui montre
l'unicité de  . Pour montrer son
existence, revenons aux égalités (4.7) et (4.9) qui
nous permettent de définir une suite
. Pour montrer son
existence, revenons aux égalités (4.7) et (4.9) qui
nous permettent de définir une suite
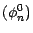 et une stratégie de
gestion
et une stratégie de
gestion
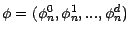 . Il
est clair que
. Il
est clair que  est autofinancée ; il reste
à montrer que
est autofinancée ; il reste
à montrer que
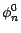 est prévisible, ce qui
résulte facilement de (4.7).
est prévisible, ce qui
résulte facilement de (4.7).
Sous-sections
Section : Sratégies autofinancées
Précédent : Remarque:
Suivant : Corollaire :
Jacques Azéma
, nous introduirons la notation
![$\displaystyle [u,v]=\sum_{k=1}^{k=d}u^kv^k=<u,v>-u^0v^0.$](img825.gif)
est une stratégie de gestion satisfaisant aux conditions de l'énoncé, les relations (
) d'éfinissant l'autofinancement sont équivalente aux égalités
est complètement déterminée par les suites
, ce qui montre l'unicité de
. Pour montrer son existence, revenons aux égalités (4.7) et (4.9) qui nous permettent de définir une suite
et une stratégie de gestion
. Il est clair que
est autofinancée ; il reste à montrer que
est prévisible, ce qui résulte facilement de (4.7).