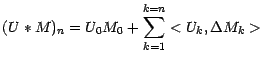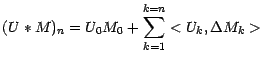Section : Proposition
Précédent : Proposition
Suivant : Proposition:
On peut donner une forme plus condensée a 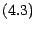 et
et 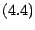 ; il suffit pour cela
d'étendre la notion de suite transformée au cas
vectoriel : revenons à la définition 3.3.1. en
supposant maintenant que
; il suffit pour cela
d'étendre la notion de suite transformée au cas
vectoriel : revenons à la définition 3.3.1. en
supposant maintenant que 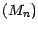 et
et 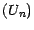 sont à valeurs dans un espace Euclidien ;
l'égalité
sont à valeurs dans un espace Euclidien ;
l'égalité
définit une suite réelle
caractérisée par les relations
Avec ces notations , 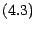 et
et 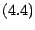 s'écrivent respectivement
s'écrivent respectivement

|
(4.5) |
La proposition suivante va nous montrer qu'il suffit de connaitre
la gestion des actifs à risque d'un investisseur et la
valeur initiale de son portefeuille pour en déduire la
totalité de sa stratégie de gestion.
Jacques Azéma