Section : Sratégies autofinancées
Précédent : Sratégies autofinancées
Suivant : Remarque:
La stratégie 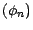 est
autofinancée si et seulement si, quelque soit
est
autofinancée si et seulement si, quelque soit 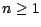 ,
,
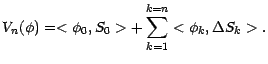
|
(4.3) |
On notera que cette égalité est équivalente
à l'égalité "actualisée"
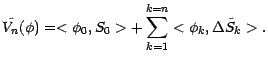
|
(4.4) |
Démonstration : Pour 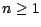 , on a
, on a
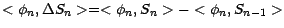 de sorte que (4.2) est équivalente aux
égalités
de sorte que (4.2) est équivalente aux
égalités
 , c'est
à dire à (4.3) .
, c'est
à dire à (4.3) .
Sous-sections
Jacques Azéma
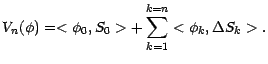
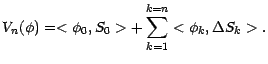
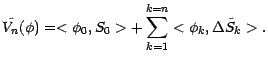
, on a
de sorte que (4.2) est équivalente aux égalités
, c'est à dire à (4.3) .