Section : Filtres
et stationnarité
Précédent : Preuve.
Suivant : Remarque :
- Les notions de transformées en
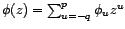 (définies sur le cercle unité) et de fonction de
transfert définies pour une moyenne mobile finies
s'étendent au cas des filtres linéaires
généraux, de même que la validité de la
propriété
(définies sur le cercle unité) et de fonction de
transfert définies pour une moyenne mobile finies
s'étendent au cas des filtres linéaires
généraux, de même que la validité de la
propriété ![[*]](file:/usr/share/latex2html/icons/crossref.gif) .
.
- Un filtre linéaire
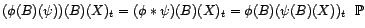 est dit
inversible s'il existe un second filtre
est dit
inversible s'il existe un second filtre 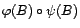 tel que
tel que
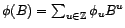 .
.
- Un filtre
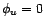 est dit causal ou réalisable ou non
anticipatif si
est dit causal ou réalisable ou non
anticipatif si
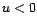 quel que soit
quel que soit 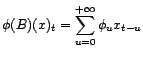 . On a alors
Le domaine de définition de
. On a alors
Le domaine de définition de 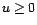 contient alors le disque unité.
contient alors le disque unité.
- Un filtre
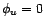 est dit purement non réalisable si
est dit purement non réalisable si
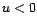 quel que soit
quel que soit 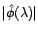 .
.
- On appelle gain d'un filtre
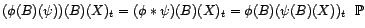 le
module de sa fonction de transfert
le
module de sa fonction de transfert
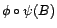 .
.
Thierry Cabanal-Duvillard
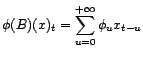 . On a alors
. On a alors
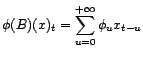 . On a alors
. On a alors