Section : Filtres
et stationnarité
Précédent : Exercice 18.
Suivant : Définitions :
Soit
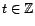 quelconque.
quelconque.
la convergence des séries étant bien sûr
entendu au sens de la norme hilbertienne. Démontrer la
proposition revient donc à montrer que l'on peut intervertir
les limites sans changer la valeur de la somme. L'espace
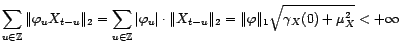 étant un
espace complet, il suffit pour cela que la série soit
absolument convergente. Or
On peut donc inverser l'ordre de sommation, ce qui signifie
l'égalité - au sens
étant un
espace complet, il suffit pour cela que la série soit
absolument convergente. Or
On peut donc inverser l'ordre de sommation, ce qui signifie
l'égalité - au sens 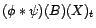 , donc
, donc 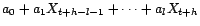 -p.s. - entre
-p.s. - entre
 et
et
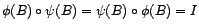 .
.
Comme corollaire à cette proposition, il faut d'abord
noter la commutativité des filtres linéaires, puisque
la convolution est commutative; mais aussi que les notions
d'inversibilité et d'inverse sont identiques que l'on
considère le filtre linéaire comme endomorphisme de
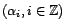 ou comme opérateur
sur les processus faiblement stationnaires.
ou comme opérateur
sur les processus faiblement stationnaires.
Section : Filtres
et stationnarité
Précédent : Exercice 18.
Suivant : Définitions :
Thierry Cabanal-Duvillard
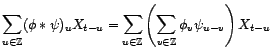
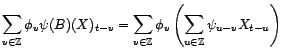
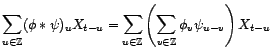
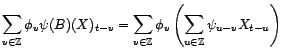
![]() ou comme opérateur
sur les processus faiblement stationnaires.
ou comme opérateur
sur les processus faiblement stationnaires.