Section : Filtres
et stationnarité
Précédent : Remarque :
Suivant : Preuve.
Soit
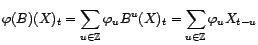 . Alors
. Alors
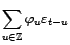 , et la
série
converge bien dans
, et la
série
converge bien dans
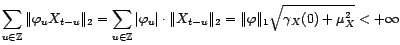 , si
, si
 est un bruit blanc. Montrer que
si de plus
est un bruit blanc. Montrer que
si de plus
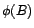 , alors la série précédente converge presque
sûrement. Indication : utiliser le lemme de Borel-Cantelli et
l'inégalité de Bienaymé-Tchebycheff.
, alors la série précédente converge presque
sûrement. Indication : utiliser le lemme de Borel-Cantelli et
l'inégalité de Bienaymé-Tchebycheff.
La proposition suivante permet de relier la convolution dans
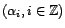 et la composition des
filtres linéaires en tant qu'opérateurs sur les
processus faiblement stationnaires.
et la composition des
filtres linéaires en tant qu'opérateurs sur les
processus faiblement stationnaires.
Thierry Cabanal-Duvillard
![]() et la composition des
filtres linéaires en tant qu'opérateurs sur les
processus faiblement stationnaires.
et la composition des
filtres linéaires en tant qu'opérateurs sur les
processus faiblement stationnaires.