Section : Définition et premières
propriétés
Précédent : Définition :
Suivant : Preuve
de la propriété
- On appelle opérateur retard, noté
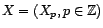 (comme Backward), l'opérateur linéaire
qui à une série temporelle
(comme Backward), l'opérateur linéaire
qui à une série temporelle
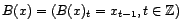 (resp. un processus
aléatoire
(resp. un processus
aléatoire
 ) fait correspondre
la série
) fait correspondre
la série
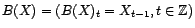 (resp. le processus
(resp. le processus
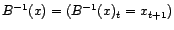 ). Cet
opérateur est inversible, et
). Cet
opérateur est inversible, et
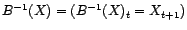 (resp.
(resp.
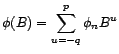 ).
).
- On appelle moyenne mobile finie tout opérateur
linéaire de la forme
avec
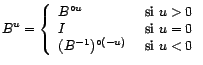 ,
et
,
et
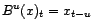 .
Ainsi,
.
Ainsi,
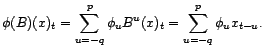 et
L'ensemble des moyennes mobiles finies forme un
et
L'ensemble des moyennes mobiles finies forme un
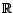 -espace vectoriel de dimension
infinie. On note
-espace vectoriel de dimension
infinie. On note 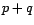 le
le 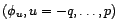 -uplet
-uplet
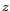 .
.
- A toute moyenne mobile finie on associe sa série de
Laurent ou transformée en
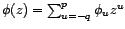
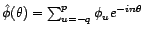 , ainsi
que sa série de Fourier ou fonction de transfert
, ainsi
que sa série de Fourier ou fonction de transfert
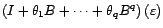 .
.
Un processus MA(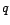 ) est donc un processus qui
peut se mettre sous la forme
) est donc un processus qui
peut se mettre sous la forme
 , avec
, avec
 bruit blanc ; tandis qu'un
processus faiblement stationnaire
bruit blanc ; tandis qu'un
processus faiblement stationnaire  est un
AR(
est un
AR( ) s'il vérifie
) s'il vérifie
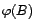 .
.
Propriété
2.II.1 Soit
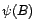 et
et 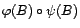 deux
moyennes mobiles finies. Alors la transformée en
deux
moyennes mobiles finies. Alors la transformée en 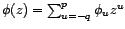 de
de
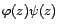 est
est
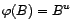 . En particulier,
. En particulier,
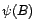 et
et 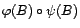 commutent. On a un résultat analogue avec la fonction de
transfert.
commutent. On a un résultat analogue avec la fonction de
transfert.
Section : Définition et premières
propriétés
Précédent : Définition :
Suivant : Preuve
de la propriété
Thierry Cabanal-Duvillard
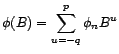 ).
).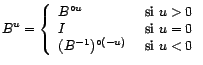 ,
,
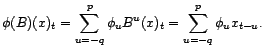 et
et
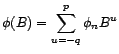 ).
).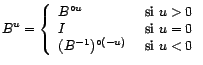 ,
,
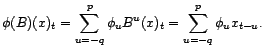 et
et
![]() ) est donc un processus qui
peut se mettre sous la forme
) est donc un processus qui
peut se mettre sous la forme
![]() , avec
, avec
![]() bruit blanc ; tandis qu'un
processus faiblement stationnaire
bruit blanc ; tandis qu'un
processus faiblement stationnaire ![]() est un
AR(
est un
AR(![]() ) s'il vérifie
) s'il vérifie![]() .
.