Section : Définition et premières
propriétés
Précédent : Définition et premières
propriétés
Suivant : Notations et définitions
On appelle processus autoregressif d'ordre  , en abrégé AR(
, en abrégé AR( ), tout
processus
), tout
processus
 faiblement
stationnaire qui vérifie
avec
faiblement
stationnaire qui vérifie
avec
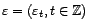 un bruit
blanc,
un bruit
blanc,
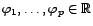 ,
,
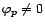 , et
, et
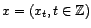 .
.
Thierry Cabanal-Duvillard