Section : Définition et premières
propriétés
Précédent : Notations et définitions
Suivant : Exercice 13.
C'est à peu près évident. Par
linéarité, on peut d'ailleurs se contenter de le
vérifier pour
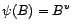 et
et
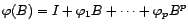 .
.
Théorème
2.II.2 Soit
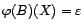 , et
, et
 un bruit blanc. Si la
transformée en
un bruit blanc. Si la
transformée en 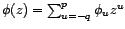 de
de
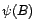 n'a pas de racine de module
égal à
n'a pas de racine de module
égal à 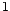 , alors il existe un et un
seul processus
, alors il existe un et un
seul processus  faiblement stationnaire tel que
faiblement stationnaire tel que
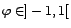 . Si de plus
. Si de plus
 est un bruit blanc fort, alors
est un bruit blanc fort, alors
 est fortement stationnaire.
est fortement stationnaire.
Provisoirement admis.
Thierry Cabanal-Duvillard
![]() et
et
![]() .
.