Section : Caractérisation des processus AR
Précédent : Exercice 14.
Suivant : Exercice 15.
Soient
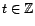 ,
, 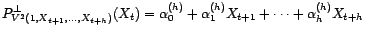 quelconques.
quelconques.
- Supposons
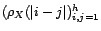 - ou, ce qui revient au
même,
- ou, ce qui revient au
même,
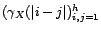 - non inversible, et montrons
que
- non inversible, et montrons
que
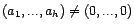 . En effet, il existe alors
. En effet, il existe alors
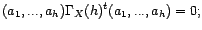 tel que
autrement dit, comme
tel que
autrement dit, comme
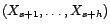 est la matrice de covariance de
tout
est la matrice de covariance de
tout 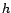 -uplet
-uplet
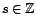 , avec
, avec
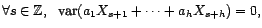 , cela signifie
ou encore
, cela signifie
ou encore
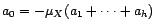
(p.s.)
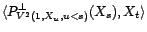
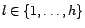 . Soit
. Soit
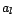 l'indice le plus grand
tel que
l'indice le plus grand
tel que  soit différent de 0. Alors, en
posant
soit différent de 0. Alors, en
posant 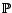 ,
, 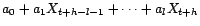 -p.s.,
-p.s.,
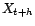 |
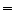 |
0 |
|
Il en résulte que 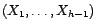 peut
s'écrire comme combinaison affine de
peut
s'écrire comme combinaison affine de
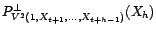 , et est donc
égal à
, et est donc
égal à
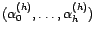 . Par
définition de la corrélation partielle, cela implique
. Par
définition de la corrélation partielle, cela implique
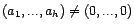 .
.
- Supposons désormais
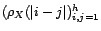 inversible,
et soit
inversible,
et soit
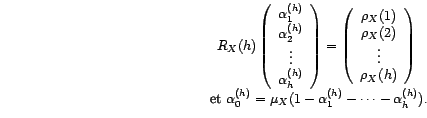 ,
déterminé par les équations de Yule-Walker de
dimension
,
déterminé par les équations de Yule-Walker de
dimension 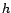 :
Si on établit que
:
Si on établit que
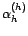 , comme la
définition de
, comme la
définition de
 ne dépend pas de
ne dépend pas de
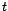 , cela montrera bien que
, cela montrera bien que
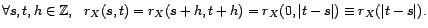 . D'après le corollaire
. D'après le corollaire
![[*]](file:/usr/share/latex2html/icons/crossref.gif) ,
les coefficients
,
les coefficients
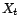 apparaissent dans la projection de
apparaissent dans la projection de 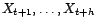 sur
sur
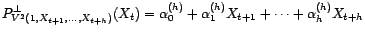 :
Or
:
Or
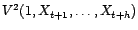 est un
sous-espace de Hilbert de
est un
sous-espace de Hilbert de
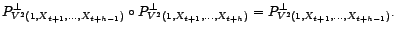 ; en
conséquence :
Il en résulte :
; en
conséquence :
Il en résulte :
Comme
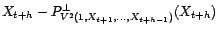 est
décorrélé avec tout élément de
est
décorrélé avec tout élément de
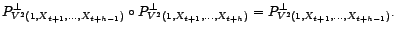 , en
particulier avec
, en
particulier avec
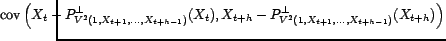 , on
en déduit
, on
en déduit
Reste donc à montrer que
On choisit, indépendamment de 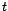 , des
coefficients
, des
coefficients
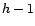 vérifiant les équations de Yule-Walker de dimension
vérifiant les équations de Yule-Walker de dimension
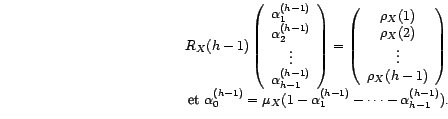 :
Alors, d'après le corollaire
:
Alors, d'après le corollaire ![[*]](file:/usr/share/latex2html/icons/crossref.gif) ,
,
D'où
Les deux variances
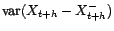 et
et
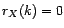 sont donc égales ; elles sont non nulles car par
hypothèse
sont donc égales ; elles sont non nulles car par
hypothèse
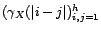 est définie positive ;
enfin leur valeur est visiblement indépendante de
est définie positive ;
enfin leur valeur est visiblement indépendante de 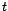 .
.
Section : Caractérisation des processus AR
Précédent : Exercice 14.
Suivant : Exercice 15.
Thierry Cabanal-Duvillard
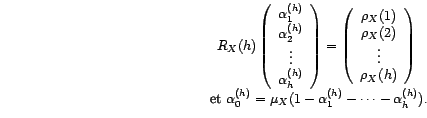 ,
déterminé par les équations de Yule-Walker de
dimension
,
déterminé par les équations de Yule-Walker de
dimension 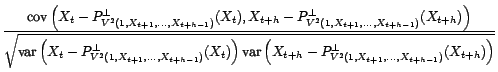
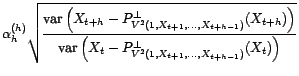
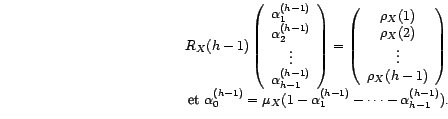 :
: