Section : Caractérisation des processus AR
Précédent : Définition :
Suivant : Exercice 14.
- Avec les notations précédentes, on appelle
corrélation partielle de
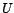 avec
avec 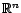 sachant
sachant
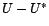 , la quantité
où on note
, la quantité
où on note
 la corrélation entre
la corrélation entre 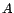 et
et 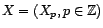 .
.
- Soit
 un processus du
second ordre. On définit sa fonction
d'autocorrélation partielle par
un processus du
second ordre. On définit sa fonction
d'autocorrélation partielle par
Exemple :
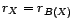 .
.
Proposition 2.II.3
Soit  est un processus faiblement
stationnaire.
est un processus faiblement
stationnaire.
-
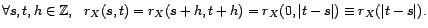 ; autrement dit,
; autrement dit,
- Si la matrice des corrélations
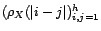 n'est pas inversible, alors
n'est pas inversible, alors 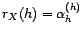 .
.
- Si
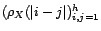 est inversible, alors
est inversible, alors
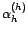 avec
avec
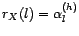 déterminé par
les équations de Yule-Walker (
déterminé par
les équations de Yule-Walker (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ).
Attention, on n'a pas
).
Attention, on n'a pas
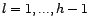 pour
pour
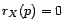 .
.
Thierry Cabanal-Duvillard
![]() .
.