La notion de prédicteur affine sert, entre autres choses,
à définir la corrélation partielle. Si ![]() et
et ![]() sont deux variables
aléatoires de carré intégrable, leur
corrélation est une mesure (imparfaite) de leur
interdépendance, autrement dit de ce que la connaissance de
l'une d'entre elles apporte comme connaissance sur l'autre. Si l'on
suppose déjà connues
sont deux variables
aléatoires de carré intégrable, leur
corrélation est une mesure (imparfaite) de leur
interdépendance, autrement dit de ce que la connaissance de
l'une d'entre elles apporte comme connaissance sur l'autre. Si l'on
suppose déjà connues ![]() autres
variables aléatoires
autres
variables aléatoires
![]() , on peut chercher à
mesurer ce que la connaissance de
, on peut chercher à
mesurer ce que la connaissance de ![]() apporte
comme renseignement supplémentaire sur
apporte
comme renseignement supplémentaire sur ![]() ,
et inversement.
,
et inversement.
Notons ![]() et
et ![]() les
prédicteurs affines au sens des moindres carrés de
les
prédicteurs affines au sens des moindres carrés de
![]() et
et ![]() sachant
sachant
![]() . Ils représentent ce
qui est connu,
. Ils représentent ce
qui est connu, ![]() et
et 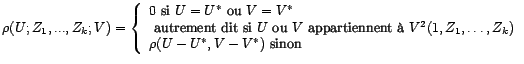 représentant ce qui reste inconnu.
représentant ce qui reste inconnu.