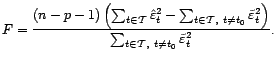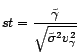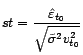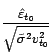Section : Modèles linéaires
Précédent : Exemple.
Suivant : Remarques :
Soit
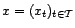 une série
temporelle, pour laquelle on a élaboré un
modèle stochastique
une série
temporelle, pour laquelle on a élaboré un
modèle stochastique
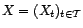 . Si le modèle
est linéaire, alors quel que soit
. Si le modèle
est linéaire, alors quel que soit
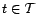 ,
,
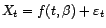 avec
avec 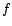 linéaire en
linéaire en
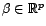 et
et
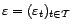 un bruit blanc
de variance
un bruit blanc
de variance
 . On note
. On note
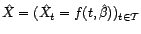 , avec
, avec
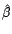 l'estimateur des moindres
carrés de
l'estimateur des moindres
carrés de 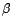 ;
; 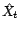 est l'estimateur des moindres carrés de
est l'estimateur des moindres carrés de
![$ {\mathbb{E}}[X_t]=f(t,{\beta})$](img226.gif) ; c'est
l'estimation de la partie déterministe du modèle. Par
; c'est
l'estimation de la partie déterministe du modèle. Par
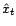 , on entendra la valeur de
, on entendra la valeur de 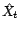 donnée par l'application
numérique. C'est la partie de la série initiale
expliquée par le modèle, celle qu'il permet de
prévoir.
donnée par l'application
numérique. C'est la partie de la série initiale
expliquée par le modèle, celle qu'il permet de
prévoir.
Soit
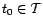 . On dira que
. On dira que 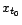 est une valeur aberrante si elle n'est pas en
accord avec le modèle ; c'est-à-dire si la
différence entre
est une valeur aberrante si elle n'est pas en
accord avec le modèle ; c'est-à-dire si la
différence entre 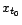 et
et
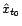 est ``trop'' grande pour que
l'on puisse valablement juger que
est ``trop'' grande pour que
l'on puisse valablement juger que 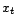 soit une
réalisation de
soit une
réalisation de
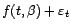 .
.
Ce peut être dû
- à une erreur de mesure, de relevé. Il est ainsi
fort probable que des erreurs se sont glissées dans les
archives du villade de Ger.
- à une perturbation ou un événement
exceptionnel. Une épidémie ou une guerre pourrait
ainsi multiplier les décès au sein du village de Ger
dans des proportions dont le modèle, qui a vocation à
expliquer la mortalité des années ordinaires et son
évolution sur le long terme, ne pourrait rendre compte.
- à une ``anomalie'' statistique. A supposer que
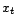 soit bien une réalisation de
soit bien une réalisation de
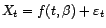 , rien
n'interdit, même si cela est peu probable, que cette valeur
soit très éloignée des valeurs médianes
prises par
, rien
n'interdit, même si cela est peu probable, que cette valeur
soit très éloignée des valeurs médianes
prises par 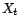 .
.
L'usage est de retirer de la série ces valeurs aberrantes
afin de ne pas perturber l'estimation des coefficients et
d'améliorer l'adéquation du modèle aux
données restantes. En quelque sorte, on corrige la
réalité pour l'adapter au modèle. D'autre
part, les valeurs aberrantes ont un intérêt pour
elles-mêmes en signalant les accidents et les bouleversements
historiques.
Pour tester si à tel instant correspond une valeur
aberrante, le test utilisé est classiquement un test de
Fisher. On introduit dans le modèle la possibilité
d'une valeur aberrante en 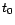 en
considérant désormais que
en
considérant désormais que 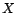 vérifie
vérifie
Tester si l'instant 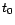 correspond à une
valeur ordinaire contre le fait que ce soit une valeur aberrante
revient à tester
correspond à une
valeur ordinaire contre le fait que ce soit une valeur aberrante
revient à tester 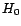 :
:
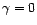 contre
contre 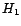 :
:
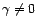 . On est ainsi ramené
à un problème classique de test d'hypothèses
linéaires. On note
. On est ainsi ramené
à un problème classique de test d'hypothèses
linéaires. On note
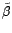 ,
,
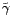 ,
,
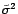 , et
, et
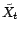 les estimateurs des moindres
carrés de
les estimateurs des moindres
carrés de 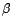 ,
, 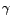 ,
,
 et
et
![$ {\mathbb{E}}[X_t]$](img241.gif) dans ce nouveau
modèle (c'est-à-dire sous
dans ce nouveau
modèle (c'est-à-dire sous 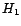 , tandis que
, tandis que
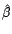 et
et 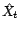 sont,
comme précédemment, les estimateurs des moindres
carrés sous
sont,
comme précédemment, les estimateurs des moindres
carrés sous 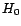 ). Soit
). Soit
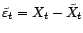 et
et
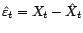 . Alors,
sous
. Alors,
sous 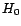 , la statistique
avec
, la statistique
avec 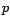 la dimension de l'espace vectoriel
engendré par
la dimension de l'espace vectoriel
engendré par
![$ {\mathbb{E}}_{{\beta},{\sigma}^2}\left[X\right]$](img244.gif) quand
quand 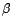 varie, et
varie, et
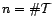 , suit une loi de Fisher
de paramètres
, suit une loi de Fisher
de paramètres 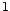 et
et 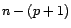 .
On en déduit un test de niveau
.
On en déduit un test de niveau 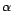 dont
la zone de rejet est de la forme
dont
la zone de rejet est de la forme
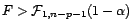 avec
avec
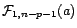 le quantile d'ordre
le quantile d'ordre
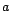 de la loi de Fisher de paramètres
de la loi de Fisher de paramètres
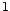 et
et 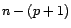 .
.
On peut donner de 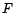 une expression un peu plus
simple. En effet, on remarque que
une expression un peu plus
simple. En effet, on remarque que
Les estimateurs des moindres carrés
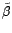 et
et
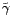 minimisent (par
définition) l'expression ci-dessus. Il s'ensuit
immédiatement que
minimisent (par
définition) l'expression ci-dessus. Il s'ensuit
immédiatement que
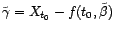 tandis que
tandis que
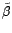 est déterminé
en minimisant
est déterminé
en minimisant
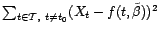 .
Autrement dit, il s'agit de l'estimateur des moindres carrés
associé au modèle
c'est-à-dire le modèle initial (sans valeur
aberrante) associé à la série
.
Autrement dit, il s'agit de l'estimateur des moindres carrés
associé au modèle
c'est-à-dire le modèle initial (sans valeur
aberrante) associé à la série 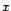 dont on a ôté le point
dont on a ôté le point 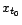 . La
statistique
. La
statistique 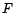 s'écrit donc
On peut donner d'autres représentations de cette
statistique. Nous avons montré à l'exercice
s'écrit donc
On peut donner d'autres représentations de cette
statistique. Nous avons montré à l'exercice ![[*]](file:/usr/share/latex2html/icons/crossref.gif) l'égalité
l'égalité 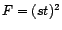 , avec
où
, avec
où
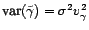 . Sous
. Sous 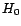 ,
, 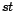 suit une loi de
Student de paramètre
suit une loi de
Student de paramètre 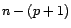 , et l'on
obtient donc les mêmes tests en considérant des zones
de rejet du type
, et l'on
obtient donc les mêmes tests en considérant des zones
de rejet du type 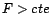 ou
ou
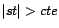 . En fait, on
peut montrer aussi que
avec
. En fait, on
peut montrer aussi que
avec
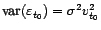 . Le test de Fisher se ramène donc un test de la forme
ce qui correspond bien à l'idée que l'on se fait
d'une valeur aberrante, à savoir qu'elle soit
déclarée telle si son résidu est excessif.
L'intérêt de cette dernière
représentation est qu'elle justifie une approximation qui
diminue fortement la complexité des calculs. En effet, telle
quelle la statistique
nécessite pour la détermination de
. Le test de Fisher se ramène donc un test de la forme
ce qui correspond bien à l'idée que l'on se fait
d'une valeur aberrante, à savoir qu'elle soit
déclarée telle si son résidu est excessif.
L'intérêt de cette dernière
représentation est qu'elle justifie une approximation qui
diminue fortement la complexité des calculs. En effet, telle
quelle la statistique
nécessite pour la détermination de
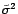 la résolution d'un
modèle linéaire pour chaque valeur de
la résolution d'un
modèle linéaire pour chaque valeur de 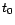 , ce qui peut finir par être fort long. En
remplaçant l'estimateur
, ce qui peut finir par être fort long. En
remplaçant l'estimateur
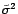 par
par
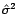 , autre estimateur de
, autre estimateur de
 , on effectue une approximation
minime qui ne perturbe pas la recherche des valeurs aberrantes.
Mais elle permet de tester tous les instants de temps en ayant
opéré qu'une seule résolution de modèle
linéaire, puisque
, on effectue une approximation
minime qui ne perturbe pas la recherche des valeurs aberrantes.
Mais elle permet de tester tous les instants de temps en ayant
opéré qu'une seule résolution de modèle
linéaire, puisque
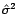 n'est pas lié à
une valeur précise
n'est pas lié à
une valeur précise 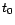 comme l'est
comme l'est
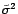 . En pratique, pour tester
au niveau
. En pratique, pour tester
au niveau 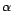 si
si 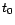 est une
valeur aberrante, on considère la zone critique de la forme
avec
est une
valeur aberrante, on considère la zone critique de la forme
avec
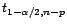 quantile d'ordre
quantile d'ordre
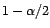 de la loi de Student de
paramètre
de la loi de Student de
paramètre 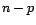 , ce qui revient à
considérer, légèrement à tort, que sous
, ce qui revient à
considérer, légèrement à tort, que sous
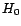
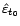 est
indépendant de
est
indépendant de
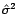 . C'est ce test, dit de
Student, qui est usuellement pratiqué. On voit dans le
tableau les degrés de signification obtenus par les deux
approches, et leur concordance.
. C'est ce test, dit de
Student, qui est usuellement pratiqué. On voit dans le
tableau les degrés de signification obtenus par les deux
approches, et leur concordance.
| Années |
Test de Fisher |
Test de Student |
| 1670 |
7,695 |
7,685 |
| 1728 |
1,567 |
1,563 |
| 1765 |
1,486 |
1,479 |
| 1796 |
1,559 |
1,555 |
Sous-sections
Section : Modèles linéaires
Précédent : Exemple.
Suivant : Remarques :
Thierry Cabanal-Duvillard
![]() une série
temporelle, pour laquelle on a élaboré un
modèle stochastique
une série
temporelle, pour laquelle on a élaboré un
modèle stochastique
![]() . Si le modèle
est linéaire, alors quel que soit
. Si le modèle
est linéaire, alors quel que soit
![]() ,
,
![]() avec
avec ![]() linéaire en
linéaire en
![]() et
et
![]() un bruit blanc
de variance
un bruit blanc
de variance
![]() . On note
. On note
![]() , avec
, avec
![]() l'estimateur des moindres
carrés de
l'estimateur des moindres
carrés de ![]() ;
; ![]() est l'estimateur des moindres carrés de
est l'estimateur des moindres carrés de
![]() ; c'est
l'estimation de la partie déterministe du modèle. Par
; c'est
l'estimation de la partie déterministe du modèle. Par
![]() , on entendra la valeur de
, on entendra la valeur de ![]() donnée par l'application
numérique. C'est la partie de la série initiale
expliquée par le modèle, celle qu'il permet de
prévoir.
donnée par l'application
numérique. C'est la partie de la série initiale
expliquée par le modèle, celle qu'il permet de
prévoir.![]() . On dira que
. On dira que ![]() est une valeur aberrante si elle n'est pas en
accord avec le modèle ; c'est-à-dire si la
différence entre
est une valeur aberrante si elle n'est pas en
accord avec le modèle ; c'est-à-dire si la
différence entre ![]() et
et
![]() est ``trop'' grande pour que
l'on puisse valablement juger que
est ``trop'' grande pour que
l'on puisse valablement juger que ![]() soit une
réalisation de
soit une
réalisation de
![]() .
.![]() en
considérant désormais que
en
considérant désormais que ![]() vérifie
vérifie
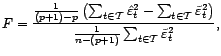
![]() une expression un peu plus
simple. En effet, on remarque que
une expression un peu plus
simple. En effet, on remarque que