Section : Détection des valeurs aberrantes
Précédent : Détection des valeurs aberrantes
Suivant : Exercice
4.
- En pratique, quelle que soit la méthode utilisée,
on ne retire les valeurs aberrantes qu'une par une, en ôtant
celle dont le degré de signification est le plus faible.
Après chaque retrait, on réestime le modèle et
les degrés de signification pour les valeurs restantes.
Ainsi, dans l'exemple précédent, on retire
l'année 1765 de l'ensemble des temps
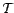 ,
et l'on refait les calculs :
,
et l'on refait les calculs :
| Années |
Test de Student |
| 1670 |
5,412 |
| 1728 |
0,857 |
| 1796 |
1,153 |
On retire alors l'année 1728 comme valeur aberrante, et
ainsi de suite.
- Sous
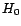 , on remarque que
Ainsi, si
, on remarque que
Ainsi, si 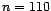 , comme dans le cas du village de
Ger, pour
, comme dans le cas du village de
Ger, pour
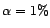 , alors
, alors
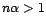 , et on peut s'attendre
à ce qu'il y ait une valeur de degré de signification
inférieur à
, et on peut s'attendre
à ce qu'il y ait une valeur de degré de signification
inférieur à  sans que cela
soit en contradiction avec
sans que cela
soit en contradiction avec 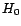 . Il faut
déduire de cet argument plus heuristique que
mathématique le fait que le seuil de degré de
signification en dessous duquel on juge une valeur aberrante doit
être faible (pas plus de
. Il faut
déduire de cet argument plus heuristique que
mathématique le fait que le seuil de degré de
signification en dessous duquel on juge une valeur aberrante doit
être faible (pas plus de  ).
).
- Au fur et à mesure que l'on retire des valeurs
aberrantes, le coefficient de détermination
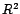 augmente, et la variance empirique
augmente, et la variance empirique
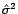 diminue. Il s'ensuit que
parmi les valeurs restantes, certaines voient leur degré de
signification baisser, et peuvent devenir à leur tour
aberrantes. Si le seuil est trop élevé, cela risque
ainsi de conduire à éliminer une proportion trop
importante de valeurs.
diminue. Il s'ensuit que
parmi les valeurs restantes, certaines voient leur degré de
signification baisser, et peuvent devenir à leur tour
aberrantes. Si le seuil est trop élevé, cela risque
ainsi de conduire à éliminer une proportion trop
importante de valeurs.
Section : Détection des valeurs aberrantes
Précédent : Détection des valeurs aberrantes
Suivant : Exercice
4.
Thierry Cabanal-Duvillard