Section : Détection des valeurs aberrantes
Précédent : Exercice 4.
Suivant : Validation du modèle
Il s'agit de montrer l'égalité
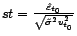 . On écrit le modèle avec valeur aberrante sous forme
matricielle régulière :
avec
. On écrit le modèle avec valeur aberrante sous forme
matricielle régulière :
avec 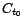 le vecteur dont toutes les
coordonnées sont nulles, sauf celle d'indice
le vecteur dont toutes les
coordonnées sont nulles, sauf celle d'indice 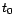 qui vaut
qui vaut 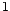 . On note
. On note 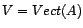 et
et
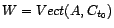 , et on pose
, et on pose
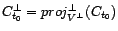 . On
rappelle que
. On
rappelle que
- Montrer que
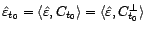 , puis que
, puis que
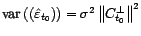 .
.
- Montrer que
 , puis que
, puis que
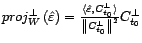 .
.
- D'après l'exercice
![[*]](file:/usr/share/latex2html/icons/crossref.gif) , on
rappelle que
, on
rappelle que
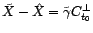 et
et
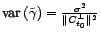 . En déduire
. En déduire
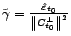 .
.
Thierry Cabanal-Duvillard