Section : Modèles linéaires avec bruit
Précédent : Modèles linéaires avec bruit
Suivant : Exercice 1.
Soit
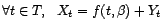 une série temporelle.
On appelle modèle linéaire avec erreur ARMA
toute modélisation de
une série temporelle.
On appelle modèle linéaire avec erreur ARMA
toute modélisation de 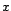 comme
réalisation d'un processus
comme
réalisation d'un processus  vérifiant
avec
vérifiant
avec 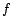 fonction linéaire du
paramètre
fonction linéaire du
paramètre
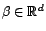 et
et 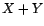 processus ARMA. Si
processus ARMA. Si 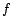 est une fonction constante
de
est une fonction constante
de 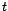 , alors on dit simplement que
, alors on dit simplement que  est un processus ARMA décentré.
est un processus ARMA décentré.
L'estimation simultanée des différents
paramètres de  est complexe. Rappelons les
résultats de l'exercice
est complexe. Rappelons les
résultats de l'exercice ![[*]](file:/usr/share/latex2html/icons/crossref.gif) : si
: si
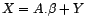 vérifie
vérifie
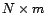 avec
avec 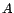 matrice
de dimensions
matrice
de dimensions 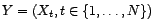 et de rang
et de rang 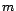 ,
,
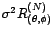 processus ARMA
processus ARMA de matrice de covariance
de matrice de covariance
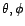 , avec
, avec
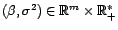 connus, et
connus, et
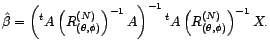 paramètres, alors l'estimateur des moindres carrés de
paramètres, alors l'estimateur des moindres carrés de
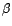 - i.e. celui qui minimise
- i.e. celui qui minimise
 -, qui est aussi l'estimateur du
maximum de vraisemblance à supposer que
-, qui est aussi l'estimateur du
maximum de vraisemblance à supposer que 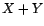 soit gaussien, est
soit gaussien, est
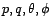
|
(41) |
Comme
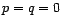 ne sont pas connus mais
doivent être estimés, on peut procèder de
manière récurrente, par approximations successives :
ne sont pas connus mais
doivent être estimés, on peut procèder de
manière récurrente, par approximations successives :
- On suppose d'abord que
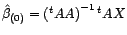 , i.e. que
, i.e. que
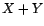 est un bruit blanc. On en déduit
l'estimation
est un bruit blanc. On en déduit
l'estimation
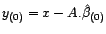 de
de 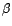 à partir de la formule ordinaire.
à partir de la formule ordinaire.
- On calcule la série temporelle
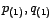 , qu'on
modélise par un processus ARMA(
, qu'on
modélise par un processus ARMA(
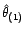 ) de paramètres
) de paramètres
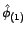 et
et
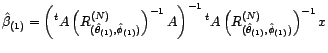 .
.
- On en déduit alors une nouvelle estimation
- On recalcule la série temporelle des erreurs
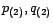 qu'on
modélise par un processus ARMA(
qu'on
modélise par un processus ARMA(
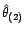 ) de paramètres
) de paramètres
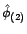 et
et
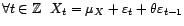 .
.
- On réitère le procédé
jusqu'à ce que les valeurs prises par les paramètres
ne se modifient sensiblement plus.
Section : Modèles linéaires avec bruit
Précédent : Modèles linéaires avec bruit
Suivant : Exercice 1.
Thierry Cabanal-Duvillard
![]() est complexe. Rappelons les
résultats de l'exercice
est complexe. Rappelons les
résultats de l'exercice ![]() : si
: si
![]() vérifie
vérifie
![]() avec
avec ![]() matrice
de dimensions
matrice
de dimensions ![]() et de rang
et de rang ![]() ,
,
![]() processus ARMA
processus ARMA![]() de matrice de covariance
de matrice de covariance
![]() , avec
, avec
![]() connus, et
connus, et
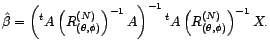 paramètres, alors l'estimateur des moindres carrés de
paramètres, alors l'estimateur des moindres carrés de
![]() - i.e. celui qui minimise
- i.e. celui qui minimise
![]() -, qui est aussi l'estimateur du
maximum de vraisemblance à supposer que
-, qui est aussi l'estimateur du
maximum de vraisemblance à supposer que ![]() soit gaussien, est
soit gaussien, est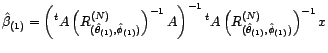 .
.