Section : Test de
Shapiro
Précédent : Test de Shapiro
Suivant : Prévision
Modèle linéaire avec
bruit corrélé. Soit
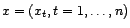 une série
temporelle associée au processus aléatoire
une série
temporelle associée au processus aléatoire
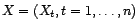 . On suppose que
. On suppose que  vérifie le modèle
vérifie le modèle 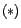 :
:
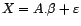 avec
avec 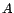 matrice de dimensions
matrice de dimensions 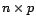 et de rang
et de rang
 ,
,
 vecteur aléatoire
centré de matrice de covariance
vecteur aléatoire
centré de matrice de covariance
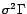 , avec
, avec  connue, et
connue, et
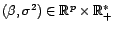 paramètres.
paramètres.
- Montrer que
 est une matrice
symétrique positive.
est une matrice
symétrique positive.
- On suppose désormais
 inversible.
Déterminer une matrice orthogonale
inversible.
Déterminer une matrice orthogonale 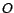 telle
que
telle
que
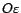 soit un vecteur dont les
composantes sont indépendantes.
soit un vecteur dont les
composantes sont indépendantes.
- En déduire une transformation du modèle
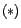 en modèle linéaire ordinaire, puis
déterminer l'estimateur des moindres carrés de
en modèle linéaire ordinaire, puis
déterminer l'estimateur des moindres carrés de 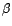 correspondant et sa matrice de covariance.
correspondant et sa matrice de covariance.
- On suppose
 gaussien. Déterminer la
fonction de vraisemblance du modèle
gaussien. Déterminer la
fonction de vraisemblance du modèle 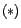 , puis
l'estimateur du maximum de vraisemblance de
, puis
l'estimateur du maximum de vraisemblance de 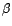 .
.
Thierry Cabanal-Duvillard