Section : Modèles linéaires avec bruit
Précédent : Définition :
Suivant : Modèles ``intégrés''
Soit
 un processus de
type MA(
un processus de
type MA(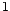 ) décentré :
avec
) décentré :
avec
 bruit blanc gaussien de
variance
bruit blanc gaussien de
variance
 et
et
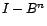 . Déterminer
l'estimateur du maximum de vraisemblance de
. Déterminer
l'estimateur du maximum de vraisemblance de 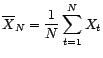 et de
et de 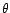 , sachant
, sachant
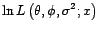 .
.
Thierry Cabanal-Duvillard
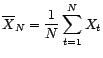 et de
et de