Section : Estimation de et
Précédent : Cas d'un processus MA()
Suivant : Cas
d'un processus ARMA()
Soit
 un processus
AR(
un processus
AR( ). D'après le théorème
). D'après le théorème
![[*]](file:/usr/share/latex2html/icons/crossref.gif) , pour tout
, pour tout 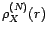 , alors
l'autocorrélation partielle empirique
, alors
l'autocorrélation partielle empirique
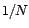 est approximativement une
gaussienne centrée de variance
est approximativement une
gaussienne centrée de variance 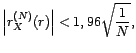 . On en
déduit comme précédemment un test de
. On en
déduit comme précédemment un test de 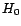 :
:  est un AR(
est un AR( ) ; si
pour (presque) tout
) ; si
pour (presque) tout 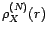 et
et  , on a
alors on accepte
, on a
alors on accepte 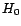 .
.
Thierry Cabanal-Duvillard
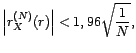 . On en
déduit comme précédemment un test de
. On en
déduit comme précédemment un test de  , on a
, on a