Section : Estimation de et
Précédent : Estimation de et
Suivant : Cas
d'un processus AR()
Soit
 un processus
MA(
un processus
MA(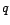 ). D'après le théorème
). D'après le théorème
![[*]](file:/usr/share/latex2html/icons/crossref.gif) , pour tout
, pour tout 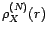 , alors
l'autocorrélation empirique
, alors
l'autocorrélation empirique
 est approximativement une
gaussienne centrée de variance
En pratique, on fait donc l'approximation
On en déduit un test (pratique mais peu rigoureux) de
est approximativement une
gaussienne centrée de variance
En pratique, on fait donc l'approximation
On en déduit un test (pratique mais peu rigoureux) de 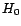 :
:  est un MA(
est un MA(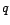 ) ; si
pour (presque) tout
) ; si
pour (presque) tout 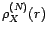 et
et  , on a
alors on accepte
, on a
alors on accepte 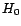 . Si l'on se limite à
. Si l'on se limite à  , c'est que l'estimation de
, c'est que l'estimation de
 devient de moins en moins
précise quand
devient de moins en moins
précise quand 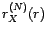 croît vers
croît vers 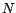 .
.
Thierry Cabanal-Duvillard
 est approximativement une
gaussienne centrée de variance
est approximativement une
gaussienne centrée de variance
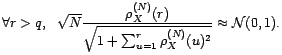
 , on a
, on a
 , c'est que l'estimation de
, c'est que l'estimation de
 devient de moins en moins
précise quand
devient de moins en moins
précise quand