Section : Estimation de et
Précédent : Cas d'un processus AR()
Suivant : Estimation des paramètres du
On pourrait s'inspirer du critère du coin pour construire un
test sur les paramètres  et
et 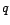 .
En pratique, on procède différemment et plus
simplement en vertu de la remarque suivante : si
.
En pratique, on procède différemment et plus
simplement en vertu de la remarque suivante : si  un processus ARMA(
un processus ARMA(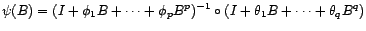 ) vérifiant
avec
) vérifiant
avec
 et
et 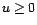 sans
racine commune, et
sans
racine commune, et
 bruit blanc d'innovation de
variance
bruit blanc d'innovation de
variance
 , alors il peut se mettre sous
forme MA(
, alors il peut se mettre sous
forme MA(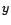 )
ou AR(
)
ou AR(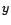 )
Comme on a les inégalités
)
Comme on a les inégalités
et que
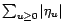 comme
comme
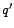 sont
finis, on en déduit qu'il est possible d'approcher d'aussi
près qu'on le souhaite
sont
finis, on en déduit qu'il est possible d'approcher d'aussi
près qu'on le souhaite  par un processus de
type MA(
par un processus de
type MA(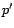 ) ou AR(
) ou AR( ) avec
) avec 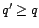 et
et 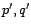 . En pratique, on
choisit pour valeurs de
. En pratique, on
choisit pour valeurs de  et
et 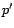 celles que l'on détermine par les méthodes
vues précédemment, en supposant le processus AR puis
MA. Cela fournit une première modélisation de
celles que l'on détermine par les méthodes
vues précédemment, en supposant le processus AR puis
MA. Cela fournit une première modélisation de  comme processus ARMA(
comme processus ARMA(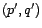 ), avec en
général plusieurs couples
), avec en
général plusieurs couples 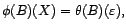 possibles. On verra par la suite comment améliorer cette
première estimation-majoration des paramètres de
``taille'' du processus ARMA.
possibles. On verra par la suite comment améliorer cette
première estimation-majoration des paramètres de
``taille'' du processus ARMA.
Section : Estimation de et
Précédent : Cas d'un processus AR()
Suivant : Estimation des paramètres du
Thierry Cabanal-Duvillard
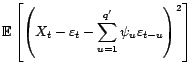
![$\displaystyle {\mathbb{E}}\left[\left(X_t-{\varepsilon}_t-\sum_{u=1}^{q'}{\psi}_u{\varepsilon}_{t-u}\right)^2\right]$](img1253.gif)
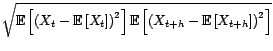

![$\displaystyle {\mathbb{E}}\left[\left(X_t-{\varepsilon}_t+\sum_{v\geq 1}^{p'}{\eta}_vX_{t-v}\right)^2\right]$](img1255.gif)