Section : Représentation causale et inversible
Précédent : Exercice 20.
Suivant : Démonstration
Soit  un processus auto-régressif d'ordre
un processus auto-régressif d'ordre
 :
avec
:
avec
 bruit blanc de variance
bruit blanc de variance
 et
et
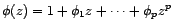 . D'après la
proposition
. D'après la
proposition ![[*]](file:/usr/share/latex2html/icons/crossref.gif) , comme la
transformée en
, comme la
transformée en 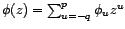 du filtre
du filtre
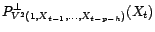 ne s'annule
pas sur le cercle unité, il existe une représentation
causale (et inversible) de
ne s'annule
pas sur le cercle unité, il existe une représentation
causale (et inversible) de  , et on peut donc
supposer que
, et on peut donc
supposer que
 est le bruit blanc d'innovation
associé à
est le bruit blanc d'innovation
associé à  . Alors, quel que soit
. Alors, quel que soit 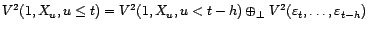 ,
,
Comme 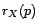 est toujours inversible, puisque
est toujours inversible, puisque
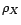 tend vers 0 en
tend vers 0 en 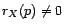 (cf
(cf ![[*]](file:/usr/share/latex2html/icons/crossref.gif) ), on
déduit de la proposition
), on
déduit de la proposition ![[*]](file:/usr/share/latex2html/icons/crossref.gif) :
:
Pour conclure cette section, le théorème suivant
complète le corollaire ![[*]](file:/usr/share/latex2html/icons/crossref.gif) , et
propose une réciproque au théorème
, et
propose une réciproque au théorème ![[*]](file:/usr/share/latex2html/icons/crossref.gif) .
.
Théorème 2.III.9 Soit
 un processus
faiblement stationnaire tel que
un processus
faiblement stationnaire tel que
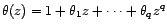 ,
avec
,
avec
 bruit blanc. Alors
bruit blanc. Alors
- Si les racines de
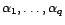 sont de module strictement plus
grand que
sont de module strictement plus
grand que 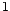 , et si les racines de
, et si les racines de
 sont de module plus grand ou
égal à
sont de module plus grand ou
égal à 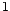 , alors
, alors
 est le bruit blanc d'innovation
de
est le bruit blanc d'innovation
de  .
.
-
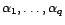 ne s'annule pas sur le cercle
unité, le filtre
ne s'annule pas sur le cercle
unité, le filtre
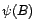 est inversible et
est inversible et  est donc un processus ARMA(
est donc un processus ARMA(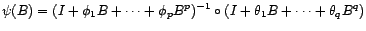 ).
).
Section : Représentation causale et inversible
Précédent : Exercice 20.
Suivant : Démonstration
Thierry Cabanal-Duvillard
![]() , et
propose une réciproque au théorème
, et
propose une réciproque au théorème ![]() .
.