Section : Représentation causale et inversible
Précédent : Démonstration du théorème
Suivant : Démonstration du corollaire
Déterminer parmi les processus suivants lesquels sont
décrits par un modèle ARMA causal ou inversible :
avec
 un bruit blanc de variance
un bruit blanc de variance
 .
.
Proposition 2.III.7
Soit
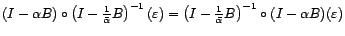 , avec
, avec
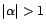 . Si
. Si
 est un bruit blanc de variance
est un bruit blanc de variance
 , alors
, alors
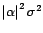 est encore un bruit blanc, de variance
est encore un bruit blanc, de variance
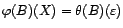 .
.
Provisoirement admis.
Corollaire 2.III.8
Soit
 un processus
ARMA(
un processus
ARMA(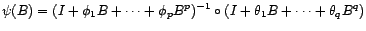 ), tel que
), tel que
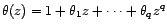 ,
avec
,
avec
 bruit blanc,
bruit blanc,
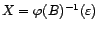 et
et
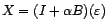 ne s'annulant
pas sur le cercle unité. Alors il existe une
représentation ARMA (
ne s'annulant
pas sur le cercle unité. Alors il existe une
représentation ARMA (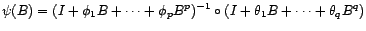 ) causale et
inversible de
) causale et
inversible de  .
.
Section : Représentation causale et inversible
Précédent : Démonstration du théorème
Suivant : Démonstration du corollaire
Thierry Cabanal-Duvillard