Section : Caractérisation des processus AR
Précédent : Exercice 15.
Suivant : Preuve
:
Soit
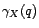 le processus MA(
le processus MA(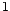 ) tel que Soit
) tel que Soit
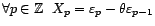 un bruit
blanc faible de variance
un bruit
blanc faible de variance
 .
avec
.
avec
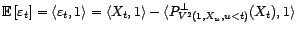 et
et
 bruit blanc de variance
bruit blanc de variance
 . Montrer que les coefficients
d'autocorrélation partielle de
. Montrer que les coefficients
d'autocorrélation partielle de  s'écrivent
s'écrivent
Théorème 2.II.4
Soit  un processus faiblement
stationnaire, dont la fonction d'autocorrélation tend vers 0
en
un processus faiblement
stationnaire, dont la fonction d'autocorrélation tend vers 0
en 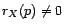 . Alors
. Alors  est un
processus AR(
est un
processus AR( ) si et seulement s'il est centré
et si
) si et seulement s'il est centré
et si
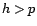 et
et 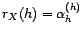 quel
que soit
quel
que soit 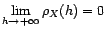 .
.
Lemme 2.II.5 Soit
 un processus faiblement stationnaire. Si
un processus faiblement stationnaire. Si
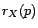 , la
matrice des corrélations
, la
matrice des corrélations 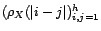 est
inversible quel que soit
est
inversible quel que soit 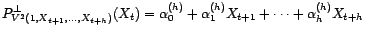 .
.
Thierry Cabanal-Duvillard