Section : Algèbres et partitions
Précédent : Algèbre engendrée par une
Suivant : Variables aléatoires -mesurables
Soit 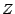 une v.a. à valeurs dans
une v.a. à valeurs dans  . L'algèbre
. L'algèbre
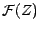 engendrée par
engendrée par 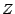 sera, par définition, l'algèbre
engendrée par la partition
sera, par définition, l'algèbre
engendrée par la partition
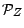 . Il est facile de voir que
Si
. Il est facile de voir que
Si 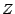 est un couple
est un couple
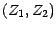 , tout atome
, tout atome
![$ [Z_{1}=k_{1}]$](img396.gif) de
de
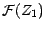 appartient à
appartient à
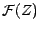 puisqu'on peut l'écrire
puisqu'on peut l'écrire
![$ \sum_{k_{2}}[Z_{1}=k_{1} ; Z_{2}=k_{2}]$](img398.gif) ; il
en résulte que
; il
en résulte que
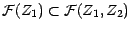
On généralise aisément par récurrence
cette situation au cas de 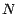 variables
aléatoires : soit
variables
aléatoires : soit
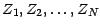 une suite de v.a.
; notons
une suite de v.a.
; notons
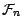 l'algèbre
l'algèbre
 . Alors
. Alors
Jacques Azéma