Section : Algèbres et partitions
Précédent : Partition engendrée par une
Suivant : Algèbre engendrée par une
- si
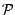 est une partition de
est une partition de  , on appellera algèbre engendrée par
, on appellera algèbre engendrée par
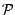 et l'on notera
et l'on notera
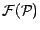 (ou plus simplement
(ou plus simplement  si aucune confusion n'est à craindre), la
classe d'événements formée des réunions
d'éléments de
si aucune confusion n'est à craindre), la
classe d'événements formée des réunions
d'éléments de 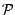 . La
donnée d'une partition est équivalente à celle
de l'algèbre qu'elle engendre; on préfère
néammoins raisonner sur les algèbres car elles
possèdent des propriétés de stabilité
relativement aux opérations booléennes que n'ont pas
les partitions. Ainsi, si
. La
donnée d'une partition est équivalente à celle
de l'algèbre qu'elle engendre; on préfère
néammoins raisonner sur les algèbres car elles
possèdent des propriétés de stabilité
relativement aux opérations booléennes que n'ont pas
les partitions. Ainsi, si 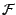 est
l'algèbre engendrée par
est
l'algèbre engendrée par 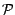 ,
On notera également que
,
On notera également que
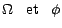 appartiennent à
appartiennent à 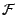
Les éléments de 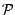 seront
appelés atomes de l'algèbre
seront
appelés atomes de l'algèbre  .
.
- Soient
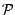 et
et 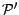 deux
partitions de
deux
partitions de  ; on dira que
; on dira que 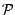 est plus fine que
est plus fine que 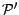 , ce
que l'on notera
, ce
que l'on notera
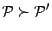 , si tout
élément de
, si tout
élément de 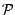 est contenu dans un
élément de
est contenu dans un
élément de 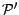 ; on vérifie
aisément que cette propriété est
équivalente á l'inclusion
; on vérifie
aisément que cette propriété est
équivalente á l'inclusion
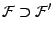 . Il en est ainsi si et
seulement si tout atome de
. Il en est ainsi si et
seulement si tout atome de  est dans
est dans
 .
.
Section : Algèbres et partitions
Précédent : Partition engendrée par une
Suivant : Algèbre engendrée par une
Jacques Azéma