Section : Algèbres et partitions
Précédent : Algèbres et partitions
Suivant : Algèbre engendrée par une
Soit 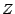 une v.a. á valeurs dans
une v.a. á valeurs dans  ; la famille finie d'événements
; la famille finie d'événements
![$ \{[Z=k]\;\;,\;\;k\in Z(\Omega )\}$](img373.gif) constitue
une partition finie de
constitue
une partition finie de  appelée
partition engendrée par
appelée
partition engendrée par 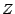 ; elle sera
notée
; elle sera
notée
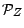 . Revenons alors à la
définition de l'epérance conditionnelle ; on a, quand
on a posé
. Revenons alors à la
définition de l'epérance conditionnelle ; on a, quand
on a posé
![$ A_{k}=[Z=k]\;\;,\;\;c_{k}=\frac{\textbf {E}[X;A_{k}]}{\textbf {P}A_{k}}$](img375.gif) On voit sur cette formule que
On voit sur cette formule que
![$ \textbf {E}[X\vert Z]$](img321.gif) ne dépend de
ne dépend de
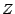 que par l'intermédiaire de la
partition qu'elle engendre . Ainsi,
puisque les partitions engendrées par
que par l'intermédiaire de la
partition qu'elle engendre . Ainsi,
puisque les partitions engendrées par
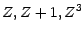 sont identiques ; en revanche,
si
sont identiques ; en revanche,
si 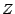 est à valeurs dans
est à valeurs dans
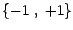 ,
,
![$ \textbf {E}[X\vert Z]$](img321.gif) et
et
![$ \textbf {E}[X\vert Z^{2}]$](img380.gif) sont
différentes. La véritable notion intéressante
est donc celle de conditionnement par une partition ; on est
conduit aux définitions suivantes :
sont
différentes. La véritable notion intéressante
est donc celle de conditionnement par une partition ; on est
conduit aux définitions suivantes :
Jacques Azéma
![$\displaystyle \textbf {E}[X\vert Z]=\sum_{k\in Z(\Omega )} c_{k}1_{A_{k}}$](img376.gif)
![$\displaystyle \textbf {E}[X\vert Z]=\sum_{k\in Z(\Omega )} c_{k}1_{A_{k}}$](img376.gif)