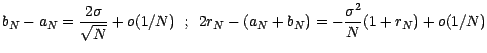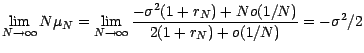Section : Une
suite de processus
Précédent : Lemme
Suivant : Les
formules de Black
Posons
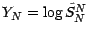 ; la suite (
; la suite ( ) converge en loi vers une gaussienne de moyenne
) converge en loi vers une gaussienne de moyenne
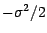 et de variance
et de variance 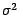 qui , rappelons le , a pour densité de
probabilité la fonction
qui , rappelons le , a pour densité de
probabilité la fonction 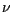 définie
sur
définie
sur
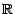 par
par
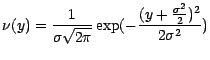
|
(7.9) |
Démonstration : On a
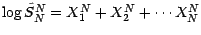 quand on a posé
quand on a posé
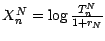
Vérifions que les suites
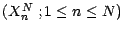 satisfont aux
hypothèses du lemme 6.2.1 :
satisfont aux
hypothèses du lemme 6.2.1 :
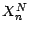 prend ses valeurs dans l'ensemble
à 2 points
prend ses valeurs dans l'ensemble
à 2 points
- les hypothèses d'indépendance sont clairement
vérifiées
- la vérification de (6.4) nécessite le calcul
suivant :
Soient 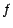 et
et
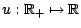 définies par
définies par
Comme 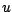 est égale à
est égale à
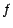 aux 2 points
aux 2 points 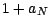 et
et 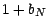 ,
,
![$ \textbf{E*}_N[f(T_1^N)]=\textbf{E*}_N[u(T_1^N)]$](img1288.gif) ; d'autre
part , puisque u est affine ,
; d'autre
part , puisque u est affine ,
On a donc , après avoir noté que
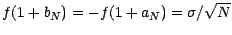 ,
,
Rappelons alors que
Il en résulte que
On a donc
ce qui , compte tenu du lemme 6.2.1 ,
démontre la proposition .
Section : Une
suite de processus
Précédent : Lemme
Suivant : Les
formules de Black
Jacques Azéma
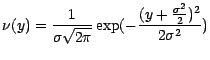
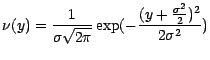
quand on a posé
satisfont aux hypothèses du lemme 6.2.1 :
et
définies par
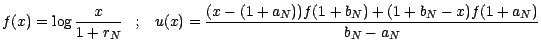
est égale à
aux 2 points
et
,
; d'autre part , puisque u est affine ,
,
![$\displaystyle \mu_N=\textbf{E*}_N[X_1^N]=\textbf{E*}_N[f(T_1^N)]=u(1+r_N)=\frac{\sigma (2r_N-(a_N+b_N))}{(b_N-a_N)\sqrt{N}}$](img1291.gif)
![$\displaystyle (1+r_N)\exp (-\frac{\sigma}{\sqrt{N}})=(1+r_N)[1-\frac{\sigma}{\sqrt{N}}+\frac{\sigma^2}{2N}+o(1/N)]$](img1293.gif)
![$\displaystyle (1+r_N)\exp (\frac{\sigma}{\sqrt{N}})=(1+r_N)[1+\frac{\sigma}{\sqrt{N}}+\frac{\sigma^2}{2N}+o(1/N)]$](img1295.gif)