Section : La
formule de Black
Précédent : Proposition
Suivant : Introduction d'une valeur initiale
Nous allons obtenir les prix des options d'achat et de vente
"à temps continu" en passant à la limite dans les
formules correspondantes du modèle de C.R.R. . Pour
une fois , nous nous intéresserons d'abord , (il y a pour
cela des raisons techniques que nous découvrirons plus bas)
, aux options de vente .
Plaçons sous la probabilité
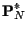 décrite dans le
paragrahe précédent ; le prix
décrite dans le
paragrahe précédent ; le prix 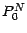 à l'instant 0 du put de prix d'exercice
à l'instant 0 du put de prix d'exercice 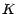 est donné par les égalités
Il s'agit maintenant d''étudier la limite de cette
quantité quand
est donné par les égalités
Il s'agit maintenant d''étudier la limite de cette
quantité quand
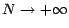 . Soit
. Soit 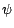 la
fonction définie par
la
fonction définie par
 ; on a
; on a
(La dernière ligne provenant de l'inégalité
entre nombres réels :
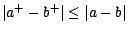 ) ; il
en résulte que
Mais , d'après la définition même de la
convergence en loi , on a , puisqe
) ; il
en résulte que
Mais , d'après la définition même de la
convergence en loi , on a , puisqe 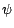 est
continue et bornée , (ce qui ne serait pas le cas pour le
calcul analogue relatif au call) ,
est
continue et bornée , (ce qui ne serait pas le cas pour le
calcul analogue relatif au call) ,
![$\displaystyle \lim_{N\to \infty}P_0^N=\int_{{\mathbb{R}}}\psi(y)\nu(y)dy=\frac{... ...\int_{{\mathbb{R}}}[Ke^{-Rt}- \exp(-\frac{\sigma^2}{2}+\sigma y)]^+e^{-y^2/2}dy$](img1310.gif)
|
(7.10) |
Sous-sections
Section : La
formule de Black
Précédent : Proposition
Suivant : Introduction d'une valeur initiale
Jacques Azéma
![$\displaystyle \lim_{N\to \infty}P_0^N=\int_{{\mathbb{R}}}\psi(y)\nu(y)dy=\frac{... ...\int_{{\mathbb{R}}}[Ke^{-Rt}- \exp(-\frac{\sigma^2}{2}+\sigma y)]^+e^{-y^2/2}dy$](img1310.gif)