Section : Les
formules de Black
Précédent : Les formules de Black
Nous avons jusqu'à présent supposé que la
valeur initiale 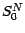 del'actif risqué
était égale à
del'actif risqué
était égale à 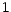 ; reprenons
maintenant les calculs au début du paragraphe 6.2 en
supposant que
; reprenons
maintenant les calculs au début du paragraphe 6.2 en
supposant que 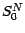 est une constante
déterministe
est une constante
déterministe 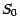 (ne dépendant pas
de
(ne dépendant pas
de 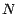 ) .
) .
Appelant  et
et 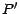 les valeurs
respectives de l'actif sous jacent et du put dans cette nouvelle
situation , on a
les valeurs
respectives de l'actif sous jacent et du put dans cette nouvelle
situation , on a
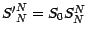 de sorte que
La limite
de sorte que
La limite 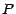 de cette expression quand
de cette expression quand 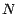 tend vers l'infini sera le prix du put dans le
modèle à temps continu ; il s'écrit , en vertu
de (6.10)
On exprime d'habitude ce résultat de façon
légèrement différente : posons
tend vers l'infini sera le prix du put dans le
modèle à temps continu ; il s'écrit , en vertu
de (6.10)
On exprime d'habitude ce résultat de façon
légèrement différente : posons

|
(7.11) |
On voit facilement que
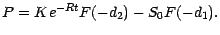 |
(7.12) |
On procède de la même façon pour définir
"à temps continu" la valeur du call de prix d'exercice 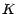 et de date d'exercice
et de date d'exercice 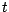 :
: 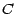 sera , par définition ,la limite des quantités
sera , par définition ,la limite des quantités 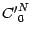 quand
quand
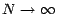 . La formule de parité
écrite pour les processus de C.R.R. conduit aux
égalités
D'où , en passant à la limite ,
. La formule de parité
écrite pour les processus de C.R.R. conduit aux
égalités
D'où , en passant à la limite ,
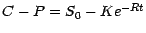 ; on a donc
; on a donc
![$ C=S_0[1-F(-d1)]-Ke^{-Rt}[1-F(-d_2)]$](img1323.gif) , ce qui
peut encore s'écrire
, ce qui
peut encore s'écrire
 |
(7.13) |
Les égalités (6.11) et (6.13) constituent les
"formules de Black and Scholes ."
Section : Les
formules de Black
Précédent : Les formules de Black
Jacques Azéma
![$\displaystyle P=\frac{S_0}{\sqrt{2\pi}}\int_{{\mathbb{R}}}[\frac{K}{S_0}e^{-Rt}... ...thbb{R}}}[Ke^{-Rt}-S_0exp(-\frac{\sigma^2}{2}+\sigma y)]^+e^{-\frac{y^2}{2}}dy $](img1317.gif)
