Section : Une
suite de processus
Précédent : Une suite de processus
Suivant : Proposition
Pour tout  , on se donne une suite
, on se donne une suite
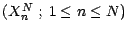 de
de 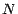 variables aléatoires indépendantes et
équidistribuées à valeurs dans l'ensemble
à 2 points
variables aléatoires indépendantes et
équidistribuées à valeurs dans l'ensemble
à 2 points
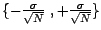 ;
on suppose en outre que l'espérance
;
on suppose en outre que l'espérance 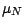 de
de
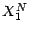 est telle que
est telle que
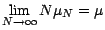 |
(7.4) |
La suite 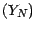 définie par
définie par
 converge
alors en loi vers une gaussienne de moyenne
converge
alors en loi vers une gaussienne de moyenne 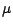 et de
variance
et de
variance 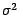 .
.
Démonstration : Si 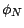 est la fonction caractéristique de
est la fonction caractéristique de 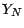 , on a
, on a
Utilisant alors le théorème de Paul
Lévy relatif à la convergence en loi , on voit qu'il
nous faut montrer que
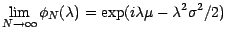
|
(7.5) |
La formule de Taylor à l'ordre 2 avec reste de
Lagrange permet d'écrire
avec
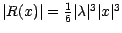 ; on a donc
; on a donc
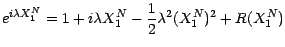
|
(7.6) |
avec
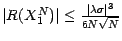 . Prenant alors l'espérance des 2 membres de (6.6) , on
obtient
. Prenant alors l'espérance des 2 membres de (6.6) , on
obtient
![$\displaystyle \textbf{E}[e^{i\lambda X_1^N}]=1+i\lambda \mu_N -\frac{\lambda^2 \sigma^2}{2N}+\textbf{E}[R(X_1^N)]$](img1266.gif)
|
(7.7) |
Mais comme
-
![$ \vert\textbf{E}[R(X_1^N)]\vert\leq \textbf{E}[\vert R(X_1^N)\vert]\leq \frac{\vert\lambda \vert^3\sigma ^3}{6N\sqrt{N}}=o(1/N)$](img1267.gif)
-
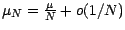 ,
,
on peut écrire
![$\displaystyle \textbf{E}[e^{i\lambda X_1^N}]=1+i\lambda \frac{\mu}{N}-\frac{\lambda ^2\sigma ^2}{2N}+o(1/N)$](img1269.gif)
|
(7.8) |
Revenons alors à l'étude de 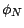 : on a
: on a
(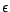 désignant une fonction
tendant vers 0 à l'origine , et le symbole
désignant une fonction
tendant vers 0 à l'origine , et le symbole 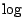 la détermination principale du logarithme
complexe) . Il ne reste plus quà faire tendre
la détermination principale du logarithme
complexe) . Il ne reste plus quà faire tendre 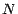 vers l'infini pour obtenir (6.5)
vers l'infini pour obtenir (6.5)
Section : Une
suite de processus
Précédent : Une suite de processus
Suivant : Proposition
Jacques Azéma
est la fonction caractéristique de
, on a
; on a donc
. Prenant alors l'espérance des 2 membres de (6.6) , on obtient
![$\displaystyle \textbf{E}[e^{i\lambda X_1^N}]=1+i\lambda \mu_N -\frac{\lambda^2 \sigma^2}{2N}+\textbf{E}[R(X_1^N)]$](img1266.gif)
![$\displaystyle \textbf{E}[e^{i\lambda X_1^N}]=1+i\lambda \frac{\mu}{N}-\frac{\lambda ^2\sigma ^2}{2N}+o(1/N)$](img1269.gif)
: on a
![$\displaystyle \exp [N\log (1+i\lambda \frac{\mu}{N}-\frac{\lambda ^2\sigma ^2}{2N}+o(1/N))]$](img1271.gif)
![$\displaystyle \exp [i\lambda \mu -\frac{\lambda^2 \sigma^2}{2}+No(1/N)+\epsilon (1/N)]$](img1272.gif)
désignant une fonction tendant vers 0 à l'origine , et le symbole
la détermination principale du logarithme complexe) . Il ne reste plus quà faire tendre
vers l'infini pour obtenir (6.5)