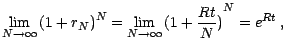Section : La
formule de Black
Précédent : Taux d'intérêt instantanés
Suivant : Lemme
Dans tout ce paragrahe , nous supposerons données 3
constantes strictement positives
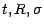 . Pour chaque entier
. Pour chaque entier 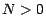 nous allons construire un marché financier
de C.R.R. de la façon suivante :
nous allons construire un marché financier
de C.R.R. de la façon suivante :
- Les valeurs des 2 actifs seront observés aux
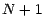 instants
instants

- Le taux d'intérêt
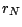 entre les
2 dates
entre les
2 dates 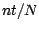 et
et 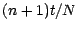 sera
égal à
sera
égal à
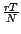 .
.
- On définit
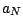 et
et 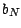 par les égalités
par les égalités
- On notera
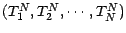 une suite de
une suite de
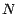 v.a. indépendantes
équidistribuées à valeurs dans
v.a. indépendantes
équidistribuées à valeurs dans
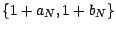 ; on supposera en outre
; on supposera en outre
![$ \textbf{E*}_N[T_1^N]=1+r_N$](img1240.gif) ce qui ,nous
l'avons vu , détermine la loi des v.a.
ce qui ,nous
l'avons vu , détermine la loi des v.a. 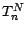 .
.
- Le cours de l'actif risqué ,noté
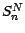 est donné par la formule
est donné par la formule
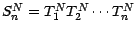 , (on suppose
, (on suppose
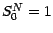 )
)
Le pas des subdivisions que nous avons construites sur ![$ [0\;t]$](img1245.gif) tend vers 0 quand
tend vers 0 quand
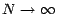 . Il parait naturel de penser
que notre suite de processus disccrets va converger (en un sens que
nous ne préciserons pas ici) vers un marché financier
à temps continu d'horizon
. Il parait naturel de penser
que notre suite de processus disccrets va converger (en un sens que
nous ne préciserons pas ici) vers un marché financier
à temps continu d'horizon 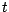 . Puisque
. Puisque
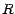 apparait comme le taux
d'intérêt instantané du processus limite .
apparait comme le taux
d'intérêt instantané du processus limite .
Pour avoir une interprétation analogue de 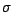 , nous aurons besoin du lemme suivant
, nous aurons besoin du lemme suivant
Sous-sections
Section : La
formule de Black
Précédent : Taux d'intérêt instantanés
Suivant : Lemme
Jacques Azéma