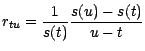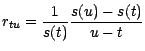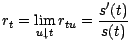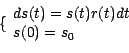Section : La
formule de Black
Précédent : La formule de Black
Suivant : Une
suite de processus
Soit
 une fonction strictement positive et dérivable
supposée représenter l'évolution des cours
d'un actif sans risque (déterministe) au cours du temps
(continu) . Si
une fonction strictement positive et dérivable
supposée représenter l'évolution des cours
d'un actif sans risque (déterministe) au cours du temps
(continu) . Si 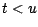 , la quantité
est le taux d'intérêt entre les instants
, la quantité
est le taux d'intérêt entre les instants 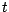 et
et 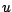 . Le taux d'intérêt
instantané
. Le taux d'intérêt
instantané 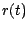 à l'instant
à l'instant 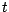 sera , par définition ,
sera , par définition ,
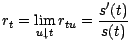
|
(7.1) |
La connaissance de la fonction
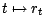 et de la valeur à
l'origine
et de la valeur à
l'origine 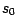 de notre actif sans risque permet
de reconstituer la fonction
de notre actif sans risque permet
de reconstituer la fonction 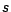 ; celle-ci est en
effet l'unique solution de l'équation différentielle
On a donc
; celle-ci est en
effet l'unique solution de l'équation différentielle
On a donc
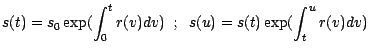
|
(7.2) |
Dans le cas où le taux instantané est une constante
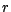 , les égalités
précédentes deviennent
, les égalités
précédentes deviennent
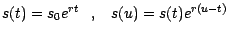 |
(7.3) |
Jacques Azéma