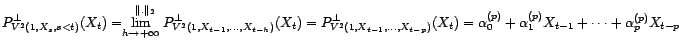Section : Caractérisation des processus AR
Précédent : Preuve :
Suivant : Exercice 17.
On suppose que  est un processus faiblement
stationnaire centré vérifiant
est un processus faiblement
stationnaire centré vérifiant
Soit
 le bruit blanc d'innovation
associé, de variance
le bruit blanc d'innovation
associé, de variance
 . Soit
. Soit 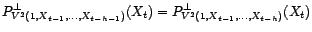 quelconque. Montrons que pour tout
quelconque. Montrons que pour tout
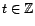 , on a :
, on a :
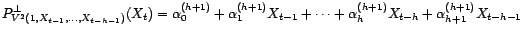
|
(23) |
En effet, on sait que
avec
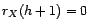 d'après la proposition
d'après la proposition ![[*]](file:/usr/share/latex2html/icons/crossref.gif) . Or
. Or
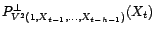 car
car 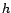 est
supérieur ou égal à
est
supérieur ou égal à  . Donc
. Donc
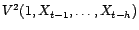 appartient
à
appartient
à
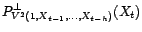 . Il en
résulte
. Il en
résulte
On déduit de (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) que pour tout
) que pour tout
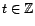
La constante
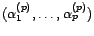 est nulle car le processus
est nulle car le processus
 est centré, et les autres
coefficients
est centré, et les autres
coefficients
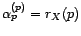 ne dépendent pas de
ne dépendent pas de 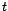 car comme on sait
ils sont déterminés par les équations de
Yule-Walker. Notons enfin que
car comme on sait
ils sont déterminés par les équations de
Yule-Walker. Notons enfin que
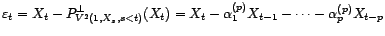 est non nul. Il en
résulte
Ceci démontre la première part du
théorème. La preuve de la réciproque est
reportée.
est non nul. Il en
résulte
Ceci démontre la première part du
théorème. La preuve de la réciproque est
reportée.
Section : Caractérisation des processus AR
Précédent : Preuve :
Suivant : Exercice 17.
Thierry Cabanal-Duvillard