Section : Caractérisation des processus MA
Précédent : Exercice 11.
Suivant : Processus AR()
Soit
 un bruit blanc de variance
un bruit blanc de variance
 , et
, et  le processus
faiblement stationnaire tel que
le processus
faiblement stationnaire tel que
- Montrer que
- En déduire que
 est le bruit blanc d'innovation
de
est le bruit blanc d'innovation
de  .
.
- Que dire de
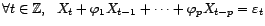 ?
?
Thierry Cabanal-Duvillard