Section : Caractérisation des processus MA
Précédent : Exercice 10.
Suivant : Exercice 11.
On suppose que  est un processus faiblement
stationnaire centré vérifiant
est un processus faiblement
stationnaire centré vérifiant
On veut montrer que  est un processus MA(
est un processus MA(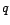 ). Soit
). Soit
 le bruit blanc d'innovation
associé, de variance
le bruit blanc d'innovation
associé, de variance
 . Comme
. Comme
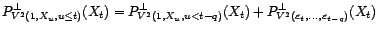 , on en déduit
, on en déduit
car 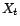 est centré,
décorrélé avec
est centré,
décorrélé avec
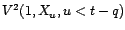 et donc orthogonal à
et donc orthogonal à
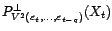 . Or,
. Or,
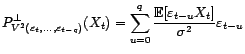 s'écrit
D'après l'exercice
s'écrit
D'après l'exercice ![[*]](file:/usr/share/latex2html/icons/crossref.gif) , la
stationnarité de
, la
stationnarité de  implique que
implique que
![$ {\mathbb{E}}[{\varepsilon}_{t-u}X_t]$](img651.gif) ne
dépende pas de
ne
dépende pas de 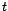 . Si on pose
alors
. Si on pose
alors
Ainsi  est-il la moyenne mobile d'ordre
est-il la moyenne mobile d'ordre 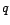 telle que
telle que
Section : Caractérisation des processus MA
Précédent : Exercice 10.
Suivant : Exercice 11.
Thierry Cabanal-Duvillard
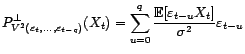 s'écrit
s'écrit