Section : Définition et premières
propriétés
Précédent : Remarques :
Suivant : Exercice
6.
Soient 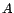 et
et 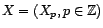 deux variables
aléatoires gaussiennes centrées réduites
indépendantes. On considère le processus stochastique
deux variables
aléatoires gaussiennes centrées réduites
indépendantes. On considère le processus stochastique
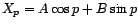 défini
par
défini
par
- Calculer la moyenne et la fonction d'autocovariance de
 . Ce processus est-il faiblement stationnaire ?
. Ce processus est-il faiblement stationnaire ?
- Déterminer la loi de
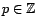 , pour tout
, pour tout
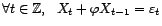 .
.
- Le processus est-il gaussien ? Est-il fortement stationnaire
?
Thierry Cabanal-Duvillard