Section : Définition et premières
propriétés
Précédent : Exercice 4.
Suivant : Exercice
5.
- Grâce aux processus stationnaires, on pourra
modéliser des phénomènes stables dans le
temps, mais autres que ceux qu'un bruit blanc permettait de
décrire.
- Un processus stationnaire du second ordre est faiblement
stationnaire.
- Un processus gaussien faiblement stationnaire est
stationnaire.
- Soit
 un processus faiblement stationnaire. Sa
fonction moyenne étant constante, on note désormais
un processus faiblement stationnaire. Sa
fonction moyenne étant constante, on note désormais
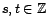 cette constante. En outre, quels que
soient
cette constante. En outre, quels que
soient
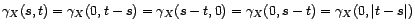 ,
La fonction d'autocovariance peut donc être simplifiée
en une fonction d'une seule variable sur
,
La fonction d'autocovariance peut donc être simplifiée
en une fonction d'une seule variable sur
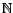 :
En particulier, quel que soit
:
En particulier, quel que soit
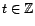 ,
,
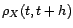 . La fonction d'autocorrélation se simplifie elle-aussi
:
. La fonction d'autocorrélation se simplifie elle-aussi
:
On notera donc
En particulier, on a toujours
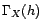 .
.
- Sous les mêmes hypothèses, on note
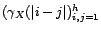 la matrice
la matrice
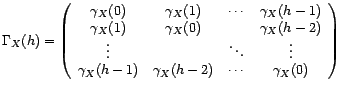 :
C'est la matrice de covariance de tout
:
C'est la matrice de covariance de tout 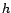 -uplet de la
forme
-uplet de la
forme
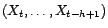 ou
ou
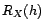 , avec
, avec
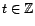 . On note de même
. On note de même 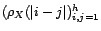 la matrice
la matrice
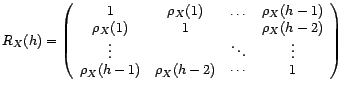 :
:
Section : Définition et premières
propriétés
Précédent : Exercice 4.
Suivant : Exercice
5.
Thierry Cabanal-Duvillard
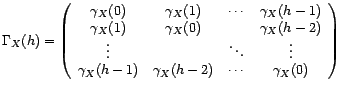 :
:
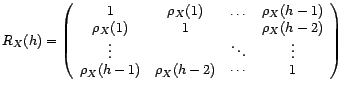 :
:
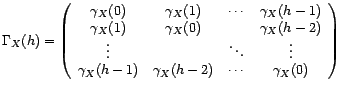 :
:
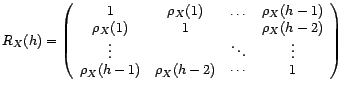 :
: