Section : Définition et premières
propriétés
Précédent : Preuve de la propriété
Suivant : Remarques :
Soit
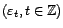 une
famille de variables aléatoires. On définit
une
famille de variables aléatoires. On définit
- On suppose que
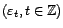 est
stationnaire. Qu'en est-il de
est
stationnaire. Qu'en est-il de  ,
, 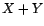 et
et 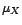 ?
?
- Même question en supposant que
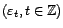 est
faiblement stationnaire.
est
faiblement stationnaire.
Thierry Cabanal-Duvillard