Section : Définition et premières
propriétés
Précédent : Exercice 2.
Suivant : Rappel.
- Soit
 un processus
aléatoire. Il est dit (fortement, strictement)
stationnaire si sa loi est invariante par translation
temporelle ; i.e. si pour tous
un processus
aléatoire. Il est dit (fortement, strictement)
stationnaire si sa loi est invariante par translation
temporelle ; i.e. si pour tous
 avec
avec 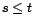 ,
,
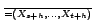 (loi)
(loi)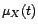
- Soit
 un processus du
second ordre. Il est dit faiblement stationnaire si sa
fonction moyenne et sa fonction d'autocovariance sont invariantes
par translation temporelle ; i.e. si pour tout
un processus du
second ordre. Il est dit faiblement stationnaire si sa
fonction moyenne et sa fonction d'autocovariance sont invariantes
par translation temporelle ; i.e. si pour tout
 ,
,
Thierry Cabanal-Duvillard