Section : Définition :
Précédent : Définition :
Suivant : Processus ARMA
Construction d'un intervalle de prévision bilatère de
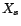 dans le cas d'un modèle gaussien.
dans le cas d'un modèle gaussien.
Soit
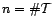 , et
, et 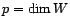 où
où 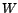 est l'espace vectoriel
engendré par
est l'espace vectoriel
engendré par
![$ {\mathbb{E}}_{{\beta},{\sigma}^2}[X]$](img392.gif) . Si le
bruit blanc
. Si le
bruit blanc
 est gaussien, alors
est gaussien, alors
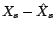 est une gaussienne
centrée de variance
est une gaussienne
centrée de variance
 , indépendante de
, indépendante de
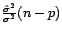 qui
suit une loi du
qui
suit une loi du 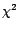 à
à 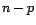 degrés de liberté. On en déduit que
degrés de liberté. On en déduit que
suit une loi de Student à 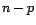 degrés de
liberté. Soit
degrés de
liberté. Soit
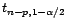 le fractile d'ordre
le fractile d'ordre
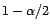 de cette loi. Alors
L'intervalle aléatoire
de cette loi. Alors
L'intervalle aléatoire
![$ \left[\hat X_s-\hat{\sigma}\sqrt{1+e^2_s},\hat X_s+\hat{\sigma}\sqrt{1+e^2_s}\right]$](img399.gif) est donc un intervalle de prévision de
est donc un intervalle de prévision de 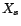 au niveau de confiance
au niveau de confiance
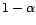 .
.
Thierry Cabanal-Duvillard
![]() , et
, et ![]() où
où ![]() est l'espace vectoriel
engendré par
est l'espace vectoriel
engendré par
![]() . Si le
bruit blanc
. Si le
bruit blanc
![]() est gaussien, alors
est gaussien, alors
![]() est une gaussienne
centrée de variance
est une gaussienne
centrée de variance
![]() , indépendante de
, indépendante de
![]() qui
suit une loi du
qui
suit une loi du ![]() à
à ![]() degrés de liberté. On en déduit que
degrés de liberté. On en déduit que
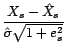
![$\displaystyle 1-{\alpha}=\P_{{\beta},{\sigma}^2}\left(\left\vert\frac{X_s-\hat ... ...s-\hat{\sigma}\sqrt{1+e^2_s},\hat X_s+\hat{\sigma}\sqrt{1+e^2_s}\right]\right) $](img398.gif)