Section : Test des
extrema locaux
Précédent : Exercice 6.
Suivant : Test du
Portemanteau
Le but de cet exercice est de définir un nouveau test de
bruit blanc.
- Rappeler les deux tests de bruit blanc vus en cours, en
précisant leurs statistiques et zones de rejet.
- Soit
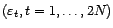 un bruit
blanc gaussien de variance
un bruit
blanc gaussien de variance 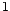 . Soit
. Soit 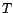 le nombre de couples
le nombre de couples
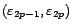 de
signe opposé,
de
signe opposé,  variant entre
variant entre 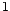 et
et 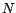 .
.
- Calculer
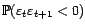 .
.
- Montrer que
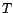 suit une loi binômiale de
paramètres
suit une loi binômiale de
paramètres 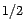 et
et 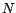 .
.
- Soit
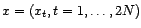 une série
chronologique. Déduire de ce qui précède un
test asymptotique de l'hypothèse
une série
chronologique. Déduire de ce qui précède un
test asymptotique de l'hypothèse 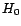 :
: 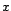 est une réalisation de bruit blanc
gaussien.
est une réalisation de bruit blanc
gaussien.
Thierry Cabanal-Duvillard
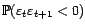 .
.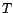 suit une loi binômiale de
paramètres
suit une loi binômiale de
paramètres 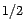 et
et 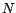 .
.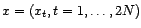 une série
chronologique. Déduire de ce qui précède un
test asymptotique de l'hypothèse
une série
chronologique. Déduire de ce qui précède un
test asymptotique de l'hypothèse 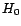 :
: 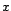 est une réalisation de bruit blanc
gaussien.
est une réalisation de bruit blanc
gaussien.