Section : Bases
hilbertiennes, et diagonalisation
Précédent : Définitions :
Suivant : Preuve
Soient
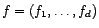 et
et
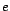 deux bases d'un espace
vectoriel
deux bases d'un espace
vectoriel 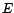 de dimension
de dimension 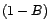 . On appelle
matrice de passage de
. On appelle
matrice de passage de 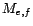 à
à 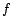 la matrice
la matrice 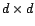 de taille
de taille 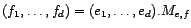 telle que
La
telle que
La
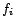 colonne
correspond aux coordonnées de
colonne
correspond aux coordonnées de 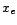 dans la
base
dans la
base 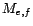 . Si
. Si 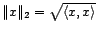 a pour
vecteur de coordonnées
a pour
vecteur de coordonnées 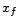 dans la base
dans la base
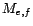 et
et 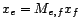 dans la base
dans la base
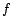 , alors
, alors
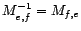 . La matrice
. La matrice 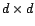 est inversible, et
est inversible, et
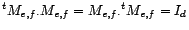 .
.
Théorème 5.III.4 Soit
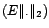 un espace de Hilbert de
dimension
un espace de Hilbert de
dimension 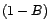 , et
, et
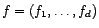 une base
hilbertienne.
une base
hilbertienne.
Proposition 5.III.5 Soit
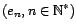 une famille libre
de
une famille libre
de 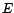 . Alors il existe une famille
orthonormée
. Alors il existe une famille
orthonormée
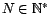 telle que, pour
tout
telle que, pour
tout
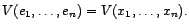 ,
Les matrices de changement de base
,
Les matrices de changement de base
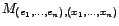 et
et
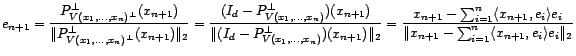 sont
triangulaires supérieures, et on a la formule de
récurrence
sont
triangulaires supérieures, et on a la formule de
récurrence
Corollaire 5.III.6 Soit 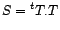 une matrice symétrique définie positive. Il existe
une matrice symétrique définie positive. Il existe
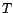 matrice triangulaire supérieure
telle que
matrice triangulaire supérieure
telle que
Section : Bases
hilbertiennes, et diagonalisation
Précédent : Définitions :
Suivant : Preuve
Thierry Cabanal-Duvillard
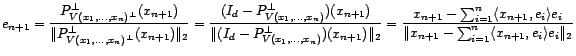 sont
triangulaires supérieures, et on a la formule de
récurrence
sont
triangulaires supérieures, et on a la formule de
récurrence