Section : Prédiction pour un processus
Précédent : Exercice 8.
Suivant : Exercice 10.
Soit
 un processus
ARIMA(1,1,1) vérifiant
avec
un processus
ARIMA(1,1,1) vérifiant
avec
 bruit blanc de variance
bruit blanc de variance
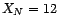 . On suppose
que
. On suppose
que 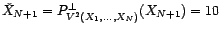 et que
et que
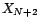 . On
suppose aussi
. On
suppose aussi 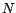 grand. Donner un intervalle de
prévision à 95% de
grand. Donner un intervalle de
prévision à 95% de 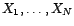 , en
supposant
, en
supposant
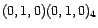 connus.
connus.
Thierry Cabanal-Duvillard